Neuroimaging: Difference between revisions
imported>Projects221 |
imported>Projects221 |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 102: | Line 102: | ||
<b> 2.</b> In order to calculate the cross correlation the Fourier transform of each file is needed. Using functions such as ‘fftn’ and ‘fftshift,’ the Fourier transform of each file is taken. <br> | <b> 2.</b> In order to calculate the cross correlation the Fourier transform of each file is needed. Using functions such as ‘fftn’ and ‘fftshift,’ the Fourier transform of each file is taken. <br> | ||
<b> 3.</b> Cross-correlation | <b> 3.</b> Cross-correlation: The maximum value of the cross-correlation is simply multiplying the Fourier transform of one file by the conjugate of the Fourier transform of the second file and then determining the maximum value. This then returns a non-normalized single value that is characteristic of how well the maximum value their image alike.<br> | ||
<b>4.</b> In order to normalize the cross-correlation, the product of the sum of the all the pixel intensities was taken. Then each maximum value from the cross-correlation was divided by the product of the sum of the vectors. This allows for the maximum value of the cross-correlation of an image with itself to be one.<br> | <b>4.</b> In order to normalize the cross-correlation, the product of the sum of the all the pixel intensities was taken. Then each maximum value from the cross-correlation was divided by the product of the sum of the vectors. This allows for the maximum value of the cross-correlation of an image with itself to be one.<br> | ||
| Line 150: | Line 150: | ||
==== Cross-Correlation ==== | ==== Cross-Correlation ==== | ||
In signal processing, cross-correlation, also known as a sliding dot product or sliding inner-product, is a measure of the similarity of two waveforms as a function of a translation applied to one of them. More formally, the 3D discrete cross-correlation of n x m x p functions f(x, y, z) and g(x, y, z) is <br> | In signal processing, cross-correlation, also known as a sliding dot product or sliding inner-product, is a measure of the similarity of two waveforms as a function of a translation applied to one of them. More formally, the 3D discrete (circular) cross-correlation of n x m x p functions f(x, y, z) and g(x, y, z) is <br> | ||
[[ File: image002.gif ]] <br><br> | [[ File: image002.gif ]] <br><br> | ||
| Line 156: | Line 156: | ||
It is maximized at the shift amount at which the signals are most similar. Therefore, a signal cross-correlated with itself, the autocorrelation, is maximized at the origin. A signal cross-correlated with a shifted version of itself is maximized at the translation amount. The maximum value of the cross-correlation provides a measure of the similarity of the two functions independent of any shifting between them. Since, for the brain-matching portion of this project, the goal is to determine if two images are of the same brain, regardless of any translation between the two acquisitions, we chose to use the maximum of the cross-correlation. <br><br> | It is maximized at the shift amount at which the signals are most similar. Therefore, a signal cross-correlated with itself, the autocorrelation, is maximized at the origin. A signal cross-correlated with a shifted version of itself is maximized at the translation amount. The maximum value of the cross-correlation provides a measure of the similarity of the two functions independent of any shifting between them. Since, for the brain-matching portion of this project, the goal is to determine if two images are of the same brain, regardless of any translation between the two acquisitions, we chose to use the maximum of the cross-correlation. <br><br> | ||
The maximum value of the cross-correlation, however, is affected by the amplitudes of f and g (in our case, the intensities of the two brain MRIs being compared. | The maximum value of the cross-correlation, however, is affected by the amplitudes of f and g (in our case, the intensities of the two brain MRIs being compared). Because our algorithm should identify two MRIs of the same brain even if they have different brightness levels (intensities), we normalize the cross-correlation maximum value before using it as our similarity metric. The cross-correlation maximum is divided by the square root of the product of the image energies. The image energy is defined as the autocorrelation at the origin, or <br> | ||
[[ File: image004.gif ]] <br> | [[ File: image004.gif ]] <br> | ||
| Line 242: | Line 242: | ||
=== Brain Matching Results === | === Brain Matching Results === | ||
The normalized cross-correlation maximum was the metric used to quantify the similarity between MRIs. This similarity between twelve randomly chosen brain MR scans are shown in the table below. This data illustrates that the values between two distinct files fall below the similarity metric threshold of 0.9 while the values of the same files are 1 (as expected due to the normalization). Therefore, | The normalized cross-correlation maximum was the metric used to quantify the similarity between MRIs. This similarity between twelve randomly chosen brain MR scans are shown in the table below. This data illustrates that the values between two distinct files fall below the similarity metric threshold of 0.9 while the values of the same files are 1 (as expected due to the normalization). Therefore, 0.9 is a | ||
reasonable choice of threshold. <br><br> | reasonable choice of threshold. <br><br> | ||
[[File: Randomvsself_Table_xCorValues.jpg|SNR - Random Vs Self|center]] <br> | [[File: Randomvsself_Table_xCorValues.jpg|SNR - Random Vs Self|center]] <br> | ||
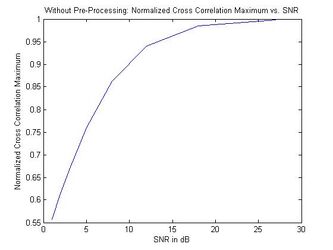
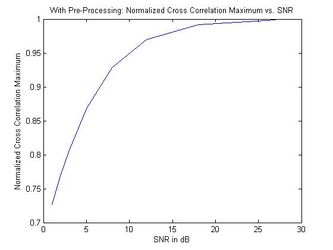
The results from adding white Gaussian noise to a randomly chosen brain MRI and comparing two different noise-added versions of the same scan are shown in the next figure. The noisy images simulate two different acquisitions of the same brain. The normalized cross-correlation maximums are plotted against the SNR of the added noise. The left plot shows the results of the cross-correlation algorithm with no pre-processing of the MRIs while the right plot shows the results from median filtering prior to cross correlation. This illustrates that, using the filtered algorithm, the images are identified as coming from the same brain | The results from adding white Gaussian noise to a randomly chosen brain MRI and comparing two different noise-added versions of the same scan are shown in the next figure. The noisy images simulate two different acquisitions of the same brain. The normalized cross-correlation maximums are plotted against the SNR of the added noise. The left plot shows the results of the cross-correlation algorithm with no pre-processing of the MRIs while the right plot shows the results from median filtering prior to cross correlation. This illustrates that, using the filtered algorithm, the images are identified as coming from the same brain (the similarity metric falls above the threshold of 0.9) as long as the SNR is above approximately 7, a significant improvement over the unfiltered algorithm. <br> <br> | ||
<center> | <center> | ||
| Line 267: | Line 267: | ||
</center> | </center> | ||
Overall, our results show that our brain matching algorithm has no false positive matches and is robust to noise and translation. Pending the availability of a dataset with multiple MRIs of the same brains, we plan to test our algorithm's ability to detect these matches. | |||
== Conclusions == | == Conclusions == | ||
| Line 306: | Line 308: | ||
<b>a)</b> Apply Wolberg and Zokai's robust image registration using log-polar transform to correct for any scaling and rotation [[#References|[4]]] Scale and rotate one of the images by the appropriate amount in order to match the other image.<br><br> | <b>a)</b> Apply Wolberg and Zokai's robust image registration using log-polar transform to correct for any scaling and rotation [[#References|[4]]] Scale and rotate one of the images by the appropriate amount in order to match the other image.<br><br> | ||
<b>b)</b> Then apply our normalized cross-correlation-based brain matching algorithm to determine the similarity between the two brains. | <b>b)</b> Then apply our normalized cross-correlation-based brain matching algorithm to determine the similarity between the two brains. <br><br> | ||
For step (a), the algorithm will have to be adapted to work in three dimensions rather than two. This should not be theoretically difficult. Spherical coordinates can be used instead of polar coordinates, still taking the log of the radial coordinate. Then, a cross-correlation that is linear in the log(r) direction and circular in the theta and phi directions will provide information on the scaling and rotation factors between the two images. The numerous 3D interpolations and cross-correlations implicit in this method, however, may pose a computational challenge. Therefore, the feasibility of making the brain matching algorithm robust to scaling and rotation should be investigated in the future if it is likely for MRIs to be rotated or scaled. | For step (a), the algorithm will have to be adapted to work in three dimensions rather than two. This should not be theoretically difficult. Spherical coordinates can be used instead of polar coordinates, still taking the log of the radial coordinate. Then, a cross-correlation that is linear in the log(r) direction and circular in the theta and phi directions will provide information on the scaling and rotation factors between the two images. The numerous 3D interpolations and cross-correlations implicit in this method, however, may pose a computational challenge. Therefore, the feasibility of making the brain matching algorithm robust to scaling and rotation should be investigated in the future if it is likely for MRIs to be rotated or scaled. | ||
| Line 380: | Line 382: | ||
Idea for using 3D Fourier transforms <br> | Idea for using 3D Fourier transforms <br> | ||
Exploration of additional filtering before cross-correlation (integrating band-pass filter and cross-correlation codes)<br> | Exploration of additional filtering before cross-correlation (integrating band-pass filter and cross-correlation codes)<br> | ||
Editing of some sections | Wiki: <br> | ||
• Writing of Algorithm Explanation and Filtering sections <br> | |||
• Editing of some sections <br> | |||
=== Acknowledgements === | === Acknowledgements === | ||
Latest revision as of 00:47, 26 March 2013
Back to Psych 221 Projects 2013
Introduction
With the opening of Stanford's Center for Cognitive and Neurobiological Imaging (CNI), we now have access to a large number of MR scans of the human brain. The CNI is closely connected to MR hardware and image processing algorithms used in the cognitive and neurobiological sciences. As a shared facility that is dedicated to research and teaching, the CNI provides resources for researchers and students. The MR images that were used for this project were obtained courtesy of the CNI.
Since the creating of the technique known as Magnetic Resonance Imaging (MRI), doctors, researches, and students alike have been utilizing its powerful capabilities to look inside the body. One key feature about an MR scan is its non-invasive technique. Using magnetic fields and radio wave pulses, the machine is able to image structures inside the body, mainly a soft tissue structures. Since the brain is soft tissue, an MR scan on the brain is ideal. Along with imaging the brain; it is able to image other objects, such as squashes. By imaging the brain, researches are able to perform tests on subjects to have greater understanding on the functions and processes of the brain.
Motivation behind the project
Brain vs Squash Detection
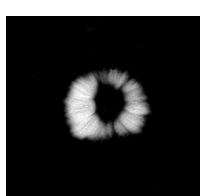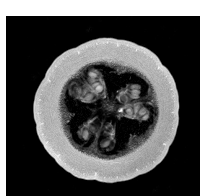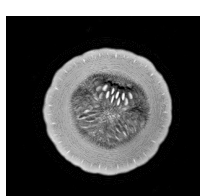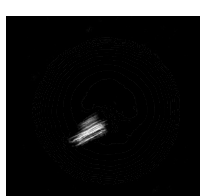
In the field of medicine, students practice taking effective MR scans on inanimate objects such as squash. In addition, researchers developing MR technology often test new techniques on objects. However, these phantom MR images often get stored into the database of actual human MR images. Sometimes the scans are labeled incorrectly, causing the contents to differ from the label and be a misleading piece of data. This proves to be a major problem and must be rectified without manually going through all of the scans. Therefore, the main motivation behind the project was to separate the scans of squash from those of brains so that there would not be trivial errors while maintaining MR databases.
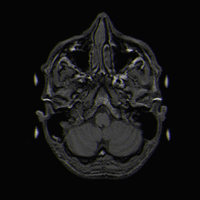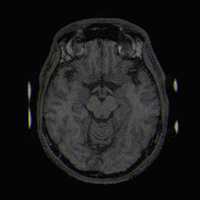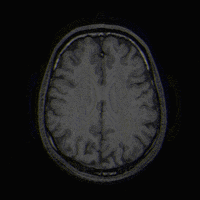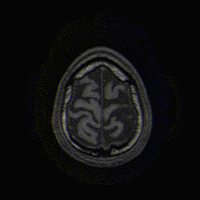
Brain vs Brain Detection
As new brains are added to existing databases, detection of MR scans taken of the same person is desirable in order to prevent duplication. In addition, efficient and accurate matching of brain MRIs may have various medical and research applications. One specific desire for matching similar brains is in order to compare data about the brain. If one were to be doing tests to understand the functionality of the brain, and two brain scans being looked at are in fact the same brain but taken at different times, then it is good to know such a fact.
Project Aim
Thus, the project was divided into two parts:
a) Brain vs. Squash detection
b) Brain vs. Brain detection
Brain vs. Squash detection
The goal of this part of the project is to determine whether a magnetic resonance scan is a brain or squash. Using striking features characteristic to each type of object, files are identified as either brain or squash images. Upon making this distinction, the squash files can be discarded and further work can be carried out on the brain scan.
Brain vs Brain matching
Identify when two MR images are of the same brain (brainprint), even if they were had different contrasts.
Dataset
Sample MR Scans
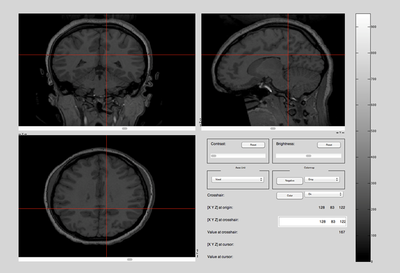
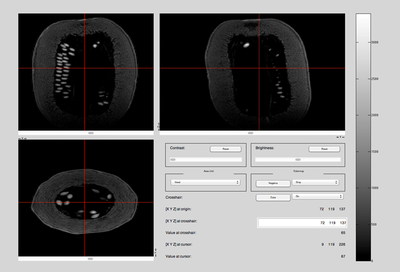
The MR scans were stored as NIFTI files. The MATLAB code available in the "Tools for NIfTI and ANALYZE images" package was used to load and initially view the MR scans. An example of a brain and a squash file is shown below. [1]
- Brain & Squash: Views
-
Top, Side, and Front View: Brain MRI
-
Top, Side, and Front View: Squash MRI
Algorithms
Brain Vs Squash Algorithm
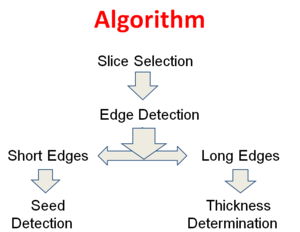
Overview
1. Select a slice from the MR image/scan
2. Perform edge detection on it. Two edges will be obtained
3. Pick short edge
a) Perform Seed Detection
i. Short Edges
ii. Fill Holes
iii. Remove Small Objects
iv. Count Pixels
v. Decide by looking at the threshold.
4. Pick long edge
a) Perform Thickness Determination
i. Calculate thickness
ii. Determine by looking at threshold
5. Combine the results from step 4 and 5.
Explanation
1. A file from the database of NIFTI files were selected in MATLAB and this data was scaled as an image and stored in a 3D array. 2D slice images (from approximately 60% up the image in the z direction) were used.
2. Edge detection on the images from the MRI was then performed. In order to execute edge detection, the built-in MATLAB edge detection functions ‘edge’ was used. Our code separates the edges returned by the function into two types of edges, long and short.
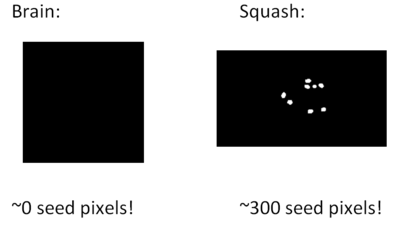
3. Since seeds were present in squashes, but not brains, they were used as one distinguishing factor. To obtain the seeds, the short edges needed to be identified.
a) Perform Seed Detection
i. In order to find seeds, short edge detection was performed on both files.
ii. For any short edge that was connected as a circle, those areas within the short edges were filled with white pixels to increase the total intensity of the files that have seeds.
iii. Small, non-seed like objects were then removed.
iv. All that remains in the image will be seeds, or bits of noise that go through the algorithm. In order to distinguish between the brain and squash file, the total number of pixels was measured. This is due to the fact that the seed pixels will be filled in, and everything else will be not.
v. Since the files with seeds have numerous pixel values, and the files without seeds do not, a threshold is set on the total number of pixels to determine which files obtain the filled in seeds. The files that give a number above the threshold are determined as seeds
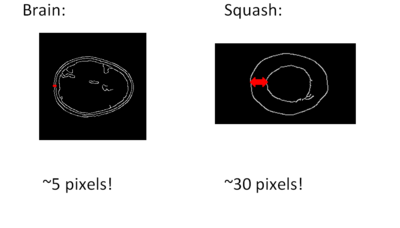
4. The other criteria to determine a squash from a brain is the measurement of the outer edges. Since a brain scan has the skull involved also, there are three distinct lines, one being the outer shell of the skull, one being the inner shell, and one being the outline of the brain. The squash on the other hand only has two long edges, and these are separated by an amount that is greater than the separation between the edges of the skull.
a) Perform Thickness Determination
i. The distance between the outer edges of both files is then determined.
ii. A threshold is then set on the number of pixels that is needed between the two long edges. If the number of pixels between the long edges is high, it is most likely a squash. If the number of pixels is low, it is most likely a brain.
5. To complete the algorithm, steps 4 and 5 are integrated to give two criteria in determining if a file is a brain or a squash.
Brain - Brain Matching Algorithm
Overview
3D Cross Correlation:
1. Take file.
2. 3D- Fourier Transform
3. Cross-correlation
i. Slide and multiply to determine similarity
3. Normalized: Robust to brightness differences! to the max intensity of each file
4. LP, HP, BP filters
5. Tests
i. Apply shifts to images
ii. Apply noise to images
6. Check Threshold
>90% similarity = MRIs of the same brain
Explanation
The main deterministic factor in the brain matching algorithm is the cross correlation. The files are three dimensional vectors; hence a three dimensional cross correlation is needed. But certain steps are taken to try and ensure a meaningful cross correlation is taken:
1. First two or more files must be selected from the NIFTI database given.
2. In order to calculate the cross correlation the Fourier transform of each file is needed. Using functions such as ‘fftn’ and ‘fftshift,’ the Fourier transform of each file is taken.
3. Cross-correlation: The maximum value of the cross-correlation is simply multiplying the Fourier transform of one file by the conjugate of the Fourier transform of the second file and then determining the maximum value. This then returns a non-normalized single value that is characteristic of how well the maximum value their image alike.
4. In order to normalize the cross-correlation, the product of the sum of the all the pixel intensities was taken. Then each maximum value from the cross-correlation was divided by the product of the sum of the vectors. This allows for the maximum value of the cross-correlation of an image with itself to be one.
5. In order to account for noise that would occur due to different acquisition times, a Low Pass Filter (LPF), Band Pass Filter (BPF) and High Pass Filter (HPF) were examined. In order to factor in a low pass filter, a threshold at 0.25〖voxels〗^(-1) was taken, thus passing information contained under 0.25〖voxels〗^(-1). The band pass filter passed any information contained in 0.25〖voxels〗^(-1) to 0.75〖voxels〗^(-1). The High pass filter passed any information contained above 0.75〖voxels〗^(-1). Each filter was implemented by finding the indices of each image where the threshold values occurred, then creating a matrix where any values outside the threshold indices are zero. This matrix was multiplied by each Fourier transform of the image to perform the actual filter.
6. In order to test the algorithm matching closely to real life situations, a shift test and noise test was performed.
i. In order to perform the shift test, MatLAB functions such as ‘circshift’ were used. The circshift function essentially loops the values from one side of the image to the other. The side of the image with the looped values was then set to zero for only the amount of indices the image was shifted. Thus, the side that in real life would be shifted off the image was replaced with zeros in order to mimic a real life shift. This shifted image was tested against the non-shifted version of the image.
ii. The second test was to add noise to a file. In order to add noise, the function ‘awgn’ was used in MatLAB. The function would add noise to a file given a certain SNR.
In order to test the cross-correlation method, one image had noise added to it, and it was tested against the same image without noise.
7. Lastly, a median filter was implemented to sift out the undesirable noise. The median filter was found at [1] and implemented into the code.
Theory / Explanation
Theory Behind Differentiating Brain and Squash
Two techniques based on detecting two key features were employed to differentiate a brain from a squash image. Firstly, the skull has thin outer layers whilst the phantoms (squash) have a thick outer layer. In addition, the squash have seeds. Edge detection was used to separate these two striking features from the rest of the contents of the brain or squash.
Edge Detection
The basic theory behind the edge detection is based on identifying the points in a digital image at which the image brightness changes sharply or, more formally, has discontinuities. These points are organized into a set of curved line segments termed edges. Since there are innate discontinuities in the MR image intensity at any change in the material properties, edge detection seems to be a good method for identifying seeds in the squash or the layers of the skull or squash. By applying an edge detector to a MRI slice, a binary image containing the set of connected curves indicating the boundaries of objects inside the scan is obtained. Hence, the application of an edge detection algorithm significantly reduces the amount of data to be processed, preserving the the important structures that are being used and filtering out information that is less relevant. This aids in efficient identification of the scan as a brain or a squash. The subsequent task would be to interpret the information contents in the original image, which is substantially simplified.
As edges in images are areas with strong intensity contrasts, the jump in intensity from one pixel to the next is exploited to our advantage. Although edge detection techniques like Prewitt, Sobel and Laplace, the Canny edge detection algorithm seems to be the optimal edge detector. The theory behind Canny edge detection can be broken down into some simple steps:
STEP 1: FILTERING.
The image is processed such that it filters out any noise in the original image. It is essential that image pre-processing is performed before trying to locate and detect any edges.
STEP 2: FINDING EDGE STRENGTH
Next, find the edge strength by taking the gradient of the image. The Sobel operator performs a 2-D spatial gradient measurement on an image. Then, the approximate absolute gradient magnitude (edge strength) at each point can be found. The Sobel operator uses a pair of 3x3 convolution masks, one estimating the gradient in the x-direction (columns) and the other estimating the gradient in the y-direction (rows). The gradient is approximated as |G| = |Gx| + |Gy|
STEP 3: FINDING EDGE DIRECTION
Once the gradient in the x and y directions are known, the edge direction can be determined. Whenever the gradient in the x direction is equal to zero, the edge direction has to be equal to 90 degrees or 0 degrees, depending on what the value of the gradient in the y-direction is equal to. If GY has a value of zero, the edge direction will equal 0 degrees. Otherwise the edge direction will equal 90 degrees. The formula for finding the edge direction is just: theta = invtan (Gy / Gx)
STEP 4: COMPARING EDGE DIRECTION
Once the edge direction is known, the next step is to relate the edge direction to a direction that can be traced in an image. So now the edge orientation has to be resolved into one of these four directions depending on which direction it is closest to.
STEP 5: HYSTERESIS
Finally, hysteresis is performed to eliminating streaking. Streaking is when the edge contour breaks due do the operator output fluctuating above and below the threshold. Once we have computed a measure of edge strength (typically the gradient magnitude), the next stage is to apply a threshold, to decide whether edges are present or not at an image point
Theory Behind Brain Matching
Cross-Correlation
In signal processing, cross-correlation, also known as a sliding dot product or sliding inner-product, is a measure of the similarity of two waveforms as a function of a translation applied to one of them. More formally, the 3D discrete (circular) cross-correlation of n x m x p functions f(x, y, z) and g(x, y, z) is
It is maximized at the shift amount at which the signals are most similar. Therefore, a signal cross-correlated with itself, the autocorrelation, is maximized at the origin. A signal cross-correlated with a shifted version of itself is maximized at the translation amount. The maximum value of the cross-correlation provides a measure of the similarity of the two functions independent of any shifting between them. Since, for the brain-matching portion of this project, the goal is to determine if two images are of the same brain, regardless of any translation between the two acquisitions, we chose to use the maximum of the cross-correlation.
The maximum value of the cross-correlation, however, is affected by the amplitudes of f and g (in our case, the intensities of the two brain MRIs being compared). Because our algorithm should identify two MRIs of the same brain even if they have different brightness levels (intensities), we normalize the cross-correlation maximum value before using it as our similarity metric. The cross-correlation maximum is divided by the square root of the product of the image energies. The image energy is defined as the autocorrelation at the origin, or
Therefore, our similarity metric S is
Due to this normalization, the S from comparing a MR scan with itself or even an intensity-scaled version of itself is 1, as desired. For example, let g(x, y, z) = βf(x, y, z). Then,
Therefore, our normalized cross-correlation-based algorithm is robust to both spatial translation and intensity differences between images.
Since a three-dimensional cross correlation in the spatial domain on 16 million voxel images would be computationally impractical, our algorithm was implemented in the frequency domain. Thus, we were able to take advantage of the computational efficiency of the 3D FFT. The 3D FFT of the cross correlation is the element-wise product of the conjugate of the 3D FFT of one image with the 3D FFT of the other:
As a result of the periodic nature of DFTs, the cross-correlation is circular. Since zero-padding the images before applying the Fourier transforms makes them 512 x 512 x 512, or 134 million voxels (far too large to take an FFT), this is not a feasible way of making the cross-correlation linear. However, since the images are already surrounded by a reasonable amount of empty space (zeros), the circular nature of our cross-correlation implementation does not appear to have a significant adverse impact on the effectiveness of our algorithm.
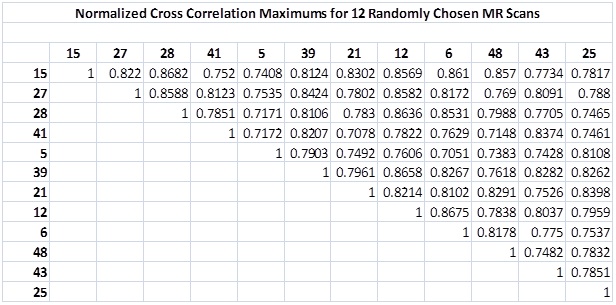
As before, we divide by the square root of the product of the image energies to obtain the values of the coefficients. The maximum value of the 3D IFFT of these coefficients is our similarity metric S. If S > 0.9, two images are deemed to have been acquired from the same brain. This choice of threshold is based on the normalized cross-correlation maximums between twelve randomly chosen images (a set of 78 values provided in the table in the Results section). It is above every S value from two distinct images.
Testing the Brain Matching Algorithm
Given the fact that multiple MR scans of the same brain were not available for the purpose of this project, the MR scans have been tampered with in two ways so as to create a 'different' brain scan from the original, such that those two scans can be compared and we can distinguish clearly between the two 'different' brain scans from the same brain.
The brain scans were tampered with in the following two ways:
I] Shifting the image:
a) Circular Shift
b) Linear Shift
II] Adding noise to the image
Shifting The Image
The idea behind shifting the image is to replicate a real life situation. Upon different acquisitions of the same brain, one may be shifted to the right, or left, or in almost any direction by a seemingly random amount. To mimic this, the ‘circshift’ in MatLAB was utilized. In order to utilize this function accurately, one side of the image needed to be replaced with zeros. This is due to the fact that the ‘circshift’ function will loop the values to the opposite side of the image in which it was shifted towards. This allows mimicking a real shift.
Adding Noise to the Image
Image-noise is the random change in brightness or color information in images. It is usually an aspect of electronic noise. It can be produced by the sensor and circuitry of a scanner or digital camera. Image noise can also originate in film grain and in the unavoidable shot noise of an ideal photon detector. Image noise is an undesirable by-product of image capture that adds spurious and extraneous information. Given the fact that multiple MR scans for the same brain we not available for the purpose of this project, the MR scans have been tempered with in two ways so as to create a 'different' brain.
For the purpose of the testing, an image was created adding gaussian noise just so that it could be differentiated from the original image. The noise added was Additive White Gaussian Noise (AWGN). AWGN is a channel model where the white noise is added with a constant spectral density. That is, the white noise has a flat or constant power spectral density. Hence, while Gaussian noise is a type of statistical noise wherein the amplitude of the noise has a Gaussian distribution, whereas Additive White Gaussian Noise is a linear combination of a Gaussian noise and a white noise. Different levels of Signal-to-Noise-Ratio were chosen at random. The images with the added noise look as follows :
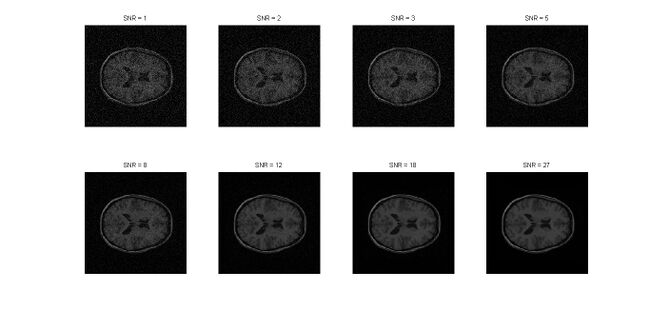
After the noise had been added to image for the purpose of testing, the technique of median filtering was employed to filter out the noise. Median filtering is a smoothing technique, where the noise is removed for optimizing the image. It is essential that we preserve the edges. However, at the same time while reducing the noise in the image, it is still essential that we preserve the edges as well. The trade-off is slight, though it still exists. The edges are of critical importance for the visual appearance of images. It has been proved that median filtering is an adequate technique for filtering out small to moderate levels of Gaussian noise as the median filter is demonstrably better than Gaussian blur at removing noise whilst preserving edges for a given, fixed window size. This is image pre-processing where the image is significantly improved as a consequence.
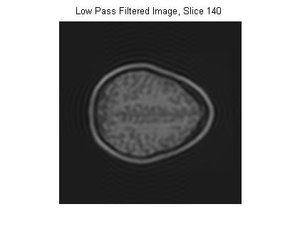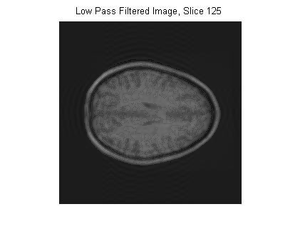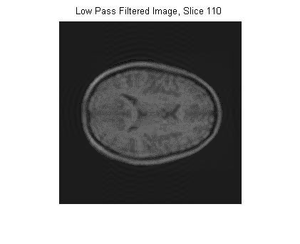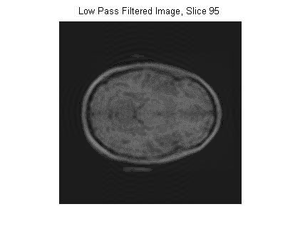
Low Pass Filtering: A low-pass filter, also called a "blurring" or "smoothing" filter, averages out rapid changes in intensity.
Low pass filtering is an attempt to get rid of any noise in an image distinguished by high frequencies. Since each acquisition of a brain, or other object, will have different noise attached to the image, the low pass filter is put in place to examine how the high frequency noise is filtered out. The one downside about a low pass filter is it naturally filters out high frequencies, which define quick changes in intensity. The other side-effect low pass filtering has is it creates ringing in the image. This ringing is described by ghost echoes of a boundary appearing in repetitive steps. This changes what the image looks like, and it allows for previous frequencies that didn’t have a strong presence in the data to now have a presence. This is due to the fact that the higher frequencies are no longer present to balance the whole image.
In order to implement the low pass filter, the values where 0.25〖voxels〗^(-1) occurred in the Fourier transform of the image was marked. Using this value, a separate matrix was created that had zeros fill the columns and rows outside the marked position. For this particular low pass filter, the cut off value was set to 0.25〖voxels〗^(-1).
High Pass Filtering:
High pass filtering is an attempt to rid the image of any low frequencies that may be undesirable. Since all the images have an initial DC component that is strongly related to the intensity of the image, it is useful to see if there is any other information represented in higher frequencies. In order to do this, a high pass filter is implemented. Unfortunately the high pass filter has some side-effects. Since it does take out the main intensity portion of the image, there isn’t much data left to gain information from. Thus the SNR is low after the high pass filter is implemented. It is implemented in the same way the low pass filter was implemented, by using a separate matrix to multiply with the Fourier transform of the image. But it only lets in frequencies above 〖0.75voxels〗^(-1).
Band Pass Filtering:
The band pass filter is a mix of the high and low pass filter. It will ideally take out all of the high frequency noise, along with the low frequency DC component that is similar in almost every image. Ideally, it will let through only the important information of an image. Nonetheless it has its own side-effects. One side-effect is it does create ringing throughout the image. The other is it filters out a large part of the image’s intensity. The good part about band-pass filtering is it allows some useful information through, and gives a different look at the image than just the high and low pass filter. The band pass filter is implemented using the low and high pass filter cut off points. But instead of placing zeros above 0.25〖voxels〗^(-1) and zeros below 0.75〖voxels〗^(-1), it inverts the method and places zeros below 0.25〖voxels〗^(-1), and zeros above 0.75〖voxels〗^(-1). This will only allow information contained in the frequencies between 0.25〖voxels〗^(-1) and 0.75〖voxels〗^(-1) through. These cut off frequencies were used in the analysis of the images.
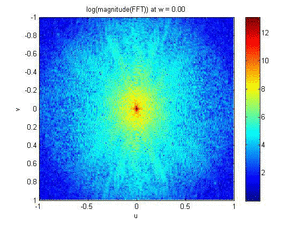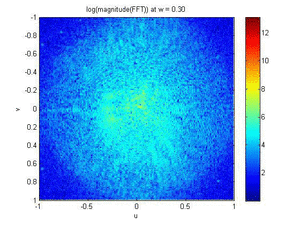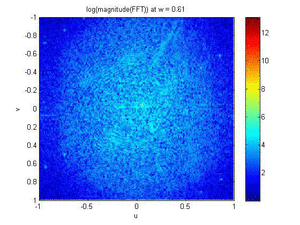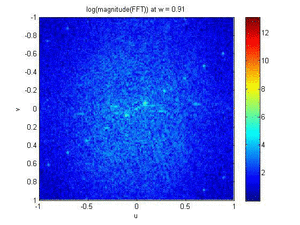
- Low Pass Filter and High Pass Filter Simulated Animations
- Band Pass Filter and Magnitude Plot (FFT) Animations
Results
Differentiating Brain and Squash Results
The figure below shows the results of the two parts of the brain-squash differentiation algorithm. The left images are from the seed detection portion. It illustrates that the seed pixels are accurately segmented in this squash MRI and no false positive pixels are marked in the brain MRI. The images on the right are from the part of the algorithm determining the thickness of the outermost layer. It illustrates that the outer layer boundaries are accurately localized. The thickness of the squash’s outer layer is significantly greater than that of the brain’s. Over all of the MR images in the sample dataset we were provided, our thresholds of 150 seed pixels and an outer layer thickness of 15 pixels proved to be safe. The two decision criteria used (number of seed pixels and outer layer thickness) were in agreement in every case, and all of the MR files were accurately classified as containing either a brain or a squash.
- Sample Differentiating Brain and Squash Results
-
Seed Detection Sample Result
-
Thickness Determination Sample Result
Brain Matching Results
The normalized cross-correlation maximum was the metric used to quantify the similarity between MRIs. This similarity between twelve randomly chosen brain MR scans are shown in the table below. This data illustrates that the values between two distinct files fall below the similarity metric threshold of 0.9 while the values of the same files are 1 (as expected due to the normalization). Therefore, 0.9 is a
reasonable choice of threshold.
The results from adding white Gaussian noise to a randomly chosen brain MRI and comparing two different noise-added versions of the same scan are shown in the next figure. The noisy images simulate two different acquisitions of the same brain. The normalized cross-correlation maximums are plotted against the SNR of the added noise. The left plot shows the results of the cross-correlation algorithm with no pre-processing of the MRIs while the right plot shows the results from median filtering prior to cross correlation. This illustrates that, using the filtered algorithm, the images are identified as coming from the same brain (the similarity metric falls above the threshold of 0.9) as long as the SNR is above approximately 7, a significant improvement over the unfiltered algorithm.
- Normalized Cross Correlation Maximum vs. SNR results
-
Normalized Cross Correlation Maximum vs. SNR (Without Pre-Processing)
-
Normalized Cross Correlation Maximum vs. SNR (With Pre-Processing)
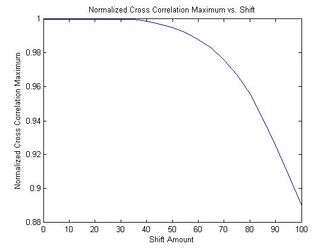
The results of linearly shifting a randomly chosen brain MRI and comparing the shifted and unshifted versions of the same scan using the filtered cross-correlation algorithm are shown below. This simulates comparing two acquisitions of the same brain. The figure plots the normalized cross-correlation maximum against the shift. It illustrates the translation-invariance of the normalized cross-correlation maximum as long as the image does not get cut off. In addition, the images are identified as coming from the same brain (the similarity metric falls above the threshold of 0.9) as long as the shift is less than approximately 95 pixels (for approximately 256x256x256 images).
- Normalized Cross Correlation Maximum vs Shift
-
Normalized Cross Correlation Maximum vs Shift
Overall, our results show that our brain matching algorithm has no false positive matches and is robust to noise and translation. Pending the availability of a dataset with multiple MRIs of the same brains, we plan to test our algorithm's ability to detect these matches.
Conclusions
Initial Struggles
Brain vs Squash Metric
The initial algorithms were about taking slices of the brain near the eyes or the teeth. After obtaining this slice, comparing the eyes or the teeth features with that of the squash and hence differentiate between the two. However, taking a slice near the eyes or the teeth in 3D was a challenge and that it was not an efficient method of distinguishing as even though the eyes and the teeth were striking features, they were not entirely ideal for identification.
Brain vs Brain metric
The initial plan was to record the outer shape of the two brain MR images. If these recorded shapes were similar, then an overlap the two MR images would be done and subsequent difference in the images would be calculated that would then be an indicator of the similarity or the mismatch of the MR images. However, this logic was flawed as it failed to take image contrast, brightness and pixel offsets into consideration. And hence, while taking the difference of the images, even the slightest of pixel offsets would push back the results by a significant amount. Thus, this technique had to be abandoned.
What worked
Brain vs Squash
The fact that slices were taken and worked upon in the 2D domain, rather than the 3D domain helped in solving the brain vs squash detection algorithm. The algorithms employed were based on the fact that a human skull has two layers, narrowly separated and that every squash has seeds; as this is true universally, the detection was successful.
Brain vs Brain
Using the 3D Fourier transforms on the images for cross-correlation in order to spot similarity or differences between two brain images worked.
Future Scope
1] There is much more to be worked on once two brains have been identified to be similar. The areas of working on the process of evaluating the image quality seems to be a promising. The process of taking an MRI scan require patients to hold still for extended periods of time. This ranges from in length from 20 minutes to 90 minutes or more. Thus, considering the fact that the MRI scans can be affected by movement, it is often noticed that problems such as mouth tumors cannot be suitably investigated as the process of coughing or swallowing can make the images that are produced less clear. An interesting prospect would be one where the MRI scan is checked to see if it's been affected by any such kind of movement. And if an error is detected owing to movement, then that MRI scan can be deemed as a flawed one without the need to manually check it. Image registration is the process of transforming different sets of data into one coordinate system. Registration is necessary in order to be able to compare or integrate the data obtained from different measurements. This, in addition to the fact that while images are being processed, factors like noise and inaccuracies would be an interesting prospect to work on.
2] While passing the image through the bandpass filter in the project, there are ringing artifacts that appear as spurious signals near sharp transitions in a signal. These occur because of the usage of a filter with a sharp cut-off frequency. Implementing filters with a smoother cut-off frequency would be something that should be worked on.
3] As humans often have medical procedures performed on them in the course of their lifetime, they often have metallic objects such as dental crowns, dental implants and metallic orthodontic appliances surgically inserted in them. These foreign objects cause artifacts and are a common problem in head and neck MRIs. Work in the field of identifying the metal dental objects that produce artifacts on brain MRIs seems to be a potential area to work on.
[2]
4] In recent times, a process called “skull stripping” has been employed on the MR scans. This process involves removal of the scalp, skull and dura, and is an important procedure in brain image analysis. In the event that skull stripping has been performed on an MR image, then one of the metrics used in this project to identify the brain, where we check the width of the two layers of the brain will fail. Thus, in the event that skull stripping has been performed on the image, an interesting future scope for this project would be to shift focus to purely the brain matter with all the tissues, and work on differentiating it's features such as corpus callosum etcetera, from that of the squash. Image segmentation by setting appropriate threshold would be a suggested technique to follow. The removal of dura-matter while leaving brain tissue untouched is especially important when estimating cortical thickness, and could be potentially worked on. [3]
5] In the event that a MR scan is a rotated or spatially scaled version of another MRI in the database, the current brain matching algorithm will not detect them to have come from the same brain. Therefore, a future improvement would be to make the cross-correlation algorithm robust to spatial rotation or scaling. One potential method to consider is the following:
a) Apply Wolberg and Zokai's robust image registration using log-polar transform to correct for any scaling and rotation [4] Scale and rotate one of the images by the appropriate amount in order to match the other image.
b) Then apply our normalized cross-correlation-based brain matching algorithm to determine the similarity between the two brains.
For step (a), the algorithm will have to be adapted to work in three dimensions rather than two. This should not be theoretically difficult. Spherical coordinates can be used instead of polar coordinates, still taking the log of the radial coordinate. Then, a cross-correlation that is linear in the log(r) direction and circular in the theta and phi directions will provide information on the scaling and rotation factors between the two images. The numerous 3D interpolations and cross-correlations implicit in this method, however, may pose a computational challenge. Therefore, the feasibility of making the brain matching algorithm robust to scaling and rotation should be investigated in the future if it is likely for MRIs to be rotated or scaled.
References
Papers and Online Material
[1] http://www.mathworks.com/matlabcentral/fileexchange/8797
[2] http://www.lni.hc.unicamp.br/fabricio/papers/2009_Costa.pdf
[3] http://brain.oxfordjournals.org/content/130/5/1432.full.pdf
[4] http://www-cs.engr.ccny.cuny.edu/~wolberg/pub/icip00.pdf
[5] http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=06098259
[6] http://noodle.med.yale.edu/~wang/Research/cviu03_wang.pdf
Software
MATLAB [R2013a (Version 8.1)]
Jasc Animation Shop
Appendix I
Source code, Sample Files, and Figures
Neuroimaging: Media: Neuroimaging.zip
Folders Contained:
•Sample NII Files and NIFTI Code
•Brain Matching Code and Results Figures
•Fourier Transform and Filtering Code and Images
•Squash Brain Differentiation Code
•Future Scope Code - Rotation and Scaling
Neuroimaging: Media: BrainMatching.zip
Appendix II
Work breakdown
Aparna Bhat
Literature search of brain matching algorithms
Research on theory behind algorithms
Idea for using thickness for differentiating brain and squash
Research on theory for future scope of the project
Documentation and Wikipedia:
• First draft of Wikipedia page
• Creation of animated figures
• Layout and formatting
• Addition of images (thumbnails and image galleries)
MATLAB code:
• Selection of random files
• Automatic file selection without user involvement
• Helped with shifting images and creating a table of cross-correlation values
• Helped with various graphs and plots
Anjali Datta
MATLAB: Neuroimaging.zip
• Downloading, opening, and viewing *.nii files
• Brain vs. squash algorithm
• Visualization of Fourier transforms: shifting, labeling, scaling, and plotting (using imagesc)
• Low-pass, band-pass, and high-pass filtering of MRIs
• Cross correlation algorithm
• Pre-processing (using medfilt3 function) before cross correlation
• Generation of data and figures: cross-correlation vs. SNR, cross-correlation vs. shift, and cross-correlation table
Literature search on cross correlation algorithms
Research on NIFTI format
Idea for using seed detection for differentiating brain and squash
Idea for cross-correlation algorithm
Exploration of cross-correlation algorithm robust to rotation and scaling
Wiki:
• Cross-correlation theory section
• Writing of results section (image galleries by Aparna)
• Editing of some sections
Andrew Zabel
MATLAB: Portions of the code in BrainMatching.zip
• 3D Fourier transforms (using fftn function) and plotting (using mesh)
• Addition of noise to images (using awgn function)
• Helped with shifting images and creating a table of cross-correlation values
• Helped with various graphs and plots
Idea for using 3D Fourier transforms
Exploration of additional filtering before cross-correlation (integrating band-pass filter and cross-correlation codes)
Wiki:
• Writing of Algorithm Explanation and Filtering sections
• Editing of some sections
Acknowledgements
Help and advice from:
• Professor Brian A. Wandell
• Professor Joyce Farrell
• Professor Robert Dougherty, Research Director Stanford Center for Neurobiological Imaging.
• Henryk Blasinski, Teaching Assistant.