RayChenPsych2012Project: Difference between revisions
imported>Psych2012 |
imported>Psych2012 |
||
| (22 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
= Background = | = Background = | ||
The human visual system features color constancy, meaning that the perceived color of objects remain relatively constant under varying lighting conditions. This helps us identify objects, as our brain lets us recognize an object as being a consistent color regardless of lighting environments. For example, a red shirt will look red under direct sunlight, but it will also look red indoors under fluorescent light. | The human visual system features color constancy, meaning that the perceived color of objects remain relatively constant under varying lighting conditions. This helps us identify objects, as our brain lets us recognize an object as being a consistent color regardless of lighting environments. For example, a red shirt will look red under direct sunlight, but it will also look red indoors under fluorescent light. | ||
| Line 13: | Line 12: | ||
A simple but effective algorithm is Gray World. This method is based on Buchsbaum's explanation of the human visual system's color constancy property, which assumes that the average reflectance of a real world scene is gray. Meaning that according to Buchsbaum, if we were to take an image with a large amount of color variations, the average value of R, G, B components should always average out to gray. The key point here is that any deviations from this average is caused by the effects of the light source. | A simple but effective algorithm is Gray World. This method is based on Buchsbaum's explanation of the human visual system's color constancy property, which assumes that the average reflectance of a real world scene is gray. Meaning that according to Buchsbaum, if we were to take an image with a large amount of color variations, the average value of R, G, B components should always average out to gray. The key point here is that any deviations from this average is caused by the effects of the light source. | ||
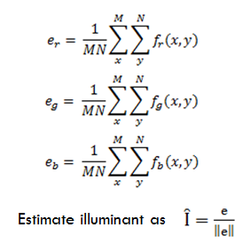
In other words, if we took a picture under orange lighting, the output image would appear more orange throughout, effectively disturbing the Gray World assumption. If we were to take this image and rescale the RGB components to average out to gray, then we should be able to remove the effects of the orange light. To do this, we just scale the RGB values of the input image by the average of the RGB values (calculated using the equations below) relative to the average of the gray value. | In other words, if we took a picture under orange lighting, the output image would appear more orange throughout, effectively disturbing the Gray World assumption. If we were to take this image and rescale the RGB components to average out to gray, then we should be able to remove the effects of the orange light. To do this, we just scale the RGB values of the input image by the average of the RGB values (calculated using the equations below) relative to the average of the gray value. f is our original input image, where the subscripts denote the color channel. | ||
<center>[[File:rc_gweqn.png |250px]]</center> | <center>[[File:rc_gweqn.png |250px]]</center> | ||
| Line 20: | Line 19: | ||
A similar algorithm to Gray World is called max-RGB. This is based on Land's theory that the human visual system achieves color constancy by detecting the area of highest reflectance in the field of view. He hypothesizes that it does this separately by the three types of cones in our eye (which detect long, medium, and short wavelengths - corresponding to R, G, and B respectively), and that we achieve color constancy by normalizing the response of each cone by their highest value. | A similar algorithm to Gray World is called max-RGB. This is based on Land's theory that the human visual system achieves color constancy by detecting the area of highest reflectance in the field of view. He hypothesizes that it does this separately by the three types of cones in our eye (which detect long, medium, and short wavelengths - corresponding to R, G, and B respectively), and that we achieve color constancy by normalizing the response of each cone by their highest value. | ||
So | So to approximate this, the Max RGB method does the same: take the maximum in each color channel and normalize the pixels in each channel according to the maximal value using the equations below. | ||
<center>[[File:rc_mrgbeqn.png |170px]]</center> | <center>[[File:rc_mrgbeqn.png |170px]]</center> | ||
= Results - | == Gray Edge & Max Edge == | ||
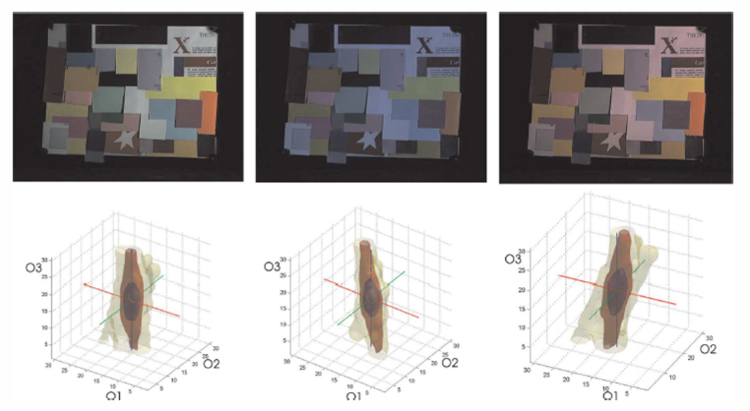
Unlike Gray World and Max-RGB, Gray Edge and Max Edge take into account the derivative structure of images; the Gray Edge hypothesis assumes that the average reflectance differences in a scene is achromatic, and Max Edge assumes that the maximum reflectance difference in a scene is achromatic. Proposed in 2007, Edge-based color constancy is based on Van De Weijer et al's observations that the distribution of derivatives of images forms a relatively regular, ellipsoid shape. The key idea here is that the long axis of this ellipsoid coincides with the illumination vector. In the figure below, we see that different types of illumination on the same scene changes the orientation of the long axis in the ellipsoid. [2] | |||
<center>[[File:rc_edgeellipsoid.png |750px]]</center> | |||
So, we can take advantage of this and estimate the illuminant using the equations below, where h is our original image passed through a Gaussian filter to reduce noise. | |||
<center>[[File:rc_edgeeqn.png |400px]]</center> | |||
We note that this uses a more generalized equation which apply to both Gray Edge (use p=1) and Max Edge (use p=infinity). This is based on Finlayson's work which generalized the Gray World and Max RGB algorithms based on the Minkowski p-norm. However, the basic theory behind these algorithms are still the same. | |||
== Gamut Mapping == | |||
I used this particular implementation [1] due to the fact that this method applies gamut mapping to the derivative structure of images. The reasoning was to compare the performance of Gray Edge and Max Edge to a more complex approach. Since I did not implement this, please refer to [1] for details on the inner workings of this algorithm. | |||
= Results = | |||
For the results, I compare the output of the algorithms to the original image generated under D65 daylight as the standard. I use the Delta E metric between these for a numerical value in difference. | |||
In image set 1 (Macbeth chart), we see that the Gray World method actually performs best due to the fact that we have a large variety of reflectance. Without comparing the results to the D65 image, we might feel that Gray Edge performs best. However, our delta E values tell a different story; if we were to examine the Gray Edge result more closely, we would see that this method is slightly biased towards a light blue. This is more apparent in the other image sets - the numbers don't lie! In image set 2, this bias in Gray Edge is more apparent, as it makes the faces look unnaturally white. Gray World no longer performs too well since a single color now dominates the image. We also see in this set that Max RGB has the best performance as in our original picture, the highest reflectance happened to be close to the illuminant. In image set 3, Max Edge dominates the performance. This is probably due to the presence of the white collar which coincided with the max edge. | |||
In image set 4, we can see that none of the algorithms perform very well. Perhaps it is due to a combination of the orange-ish illuminant and the green-ish background in the painting, but we see that all of the color balancing methods biased towards a blue background. This accounts for the high delta E values. Although the results may look acceptable by themselves (such as Max Edge), the goal is to reproduce the most similar color to the original; therefore, we can only conclude that the methods fail in this case. | |||
== | == Image set 1 == | ||
<center>[[File:rc_macbethresults.png |1200px]]</center> | |||
== Image set 2 == | |||
<center>[[File:rc_results2.png |1000px]]</center> | |||
== Image set 3 == | |||
<center>[[File:rc_results3.png |900px]]</center> | |||
== Image set 4 == | |||
<center>[[File:rc_results4.png |1200px]]</center> | |||
= Conclusions = | = Conclusions = | ||
We see from this sample of results that these algorithms are highly dependent on the input scene. Even a small area in the scene can widely affect the performance of these methods. We would need to test on a larger variety of illuminants to reach more conclusive results, especially since the edge based algorithms seem to work better for outdoor images. | |||
We also conclude that simple algorithms can achieve similar performance to more complex algorithms. While the gamut mapping method referenced in this project needs heavy computation (calibration over a set of canonical gamuts and needs to use convex optimization), the other methods described can be run in real time without having to use too much special hardware. For future work, it may be useful to see how robust a combination of these methods would be. | |||
= References - Resources and related work = | = References - Resources and related work = | ||
Latest revision as of 22:41, 19 March 2012
Background
The human visual system features color constancy, meaning that the perceived color of objects remain relatively constant under varying lighting conditions. This helps us identify objects, as our brain lets us recognize an object as being a consistent color regardless of lighting environments. For example, a red shirt will look red under direct sunlight, but it will also look red indoors under fluorescent light.
However, if we were to measure the actual reflected light coming from the shirt under these two conditions, we would see that they differ. This is where problems arise. Think about the last time you took a picture with your digital camera, and the colors just seemed wrong. This is because cameras do not have the ability of color constancy. Fortunately, we can adjust for this by using color balancing algorithms.
Methods
In this project, I explore a number of popular color balancing algorithms. Specifically, I implement Gray World, Max-RGB, and Gray-Edge. In addition, I compare the results to an existing state-of-the-art application of gamut mapping [1].
Gray World
A simple but effective algorithm is Gray World. This method is based on Buchsbaum's explanation of the human visual system's color constancy property, which assumes that the average reflectance of a real world scene is gray. Meaning that according to Buchsbaum, if we were to take an image with a large amount of color variations, the average value of R, G, B components should always average out to gray. The key point here is that any deviations from this average is caused by the effects of the light source.
In other words, if we took a picture under orange lighting, the output image would appear more orange throughout, effectively disturbing the Gray World assumption. If we were to take this image and rescale the RGB components to average out to gray, then we should be able to remove the effects of the orange light. To do this, we just scale the RGB values of the input image by the average of the RGB values (calculated using the equations below) relative to the average of the gray value. f is our original input image, where the subscripts denote the color channel.
Max RGB
A similar algorithm to Gray World is called max-RGB. This is based on Land's theory that the human visual system achieves color constancy by detecting the area of highest reflectance in the field of view. He hypothesizes that it does this separately by the three types of cones in our eye (which detect long, medium, and short wavelengths - corresponding to R, G, and B respectively), and that we achieve color constancy by normalizing the response of each cone by their highest value.
So to approximate this, the Max RGB method does the same: take the maximum in each color channel and normalize the pixels in each channel according to the maximal value using the equations below.
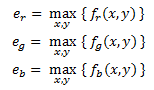
Gray Edge & Max Edge
Unlike Gray World and Max-RGB, Gray Edge and Max Edge take into account the derivative structure of images; the Gray Edge hypothesis assumes that the average reflectance differences in a scene is achromatic, and Max Edge assumes that the maximum reflectance difference in a scene is achromatic. Proposed in 2007, Edge-based color constancy is based on Van De Weijer et al's observations that the distribution of derivatives of images forms a relatively regular, ellipsoid shape. The key idea here is that the long axis of this ellipsoid coincides with the illumination vector. In the figure below, we see that different types of illumination on the same scene changes the orientation of the long axis in the ellipsoid. [2]
So, we can take advantage of this and estimate the illuminant using the equations below, where h is our original image passed through a Gaussian filter to reduce noise.
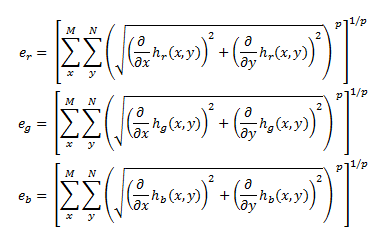
We note that this uses a more generalized equation which apply to both Gray Edge (use p=1) and Max Edge (use p=infinity). This is based on Finlayson's work which generalized the Gray World and Max RGB algorithms based on the Minkowski p-norm. However, the basic theory behind these algorithms are still the same.
Gamut Mapping
I used this particular implementation [1] due to the fact that this method applies gamut mapping to the derivative structure of images. The reasoning was to compare the performance of Gray Edge and Max Edge to a more complex approach. Since I did not implement this, please refer to [1] for details on the inner workings of this algorithm.
Results
For the results, I compare the output of the algorithms to the original image generated under D65 daylight as the standard. I use the Delta E metric between these for a numerical value in difference.
In image set 1 (Macbeth chart), we see that the Gray World method actually performs best due to the fact that we have a large variety of reflectance. Without comparing the results to the D65 image, we might feel that Gray Edge performs best. However, our delta E values tell a different story; if we were to examine the Gray Edge result more closely, we would see that this method is slightly biased towards a light blue. This is more apparent in the other image sets - the numbers don't lie! In image set 2, this bias in Gray Edge is more apparent, as it makes the faces look unnaturally white. Gray World no longer performs too well since a single color now dominates the image. We also see in this set that Max RGB has the best performance as in our original picture, the highest reflectance happened to be close to the illuminant. In image set 3, Max Edge dominates the performance. This is probably due to the presence of the white collar which coincided with the max edge.
In image set 4, we can see that none of the algorithms perform very well. Perhaps it is due to a combination of the orange-ish illuminant and the green-ish background in the painting, but we see that all of the color balancing methods biased towards a blue background. This accounts for the high delta E values. Although the results may look acceptable by themselves (such as Max Edge), the goal is to reproduce the most similar color to the original; therefore, we can only conclude that the methods fail in this case.
Image set 1
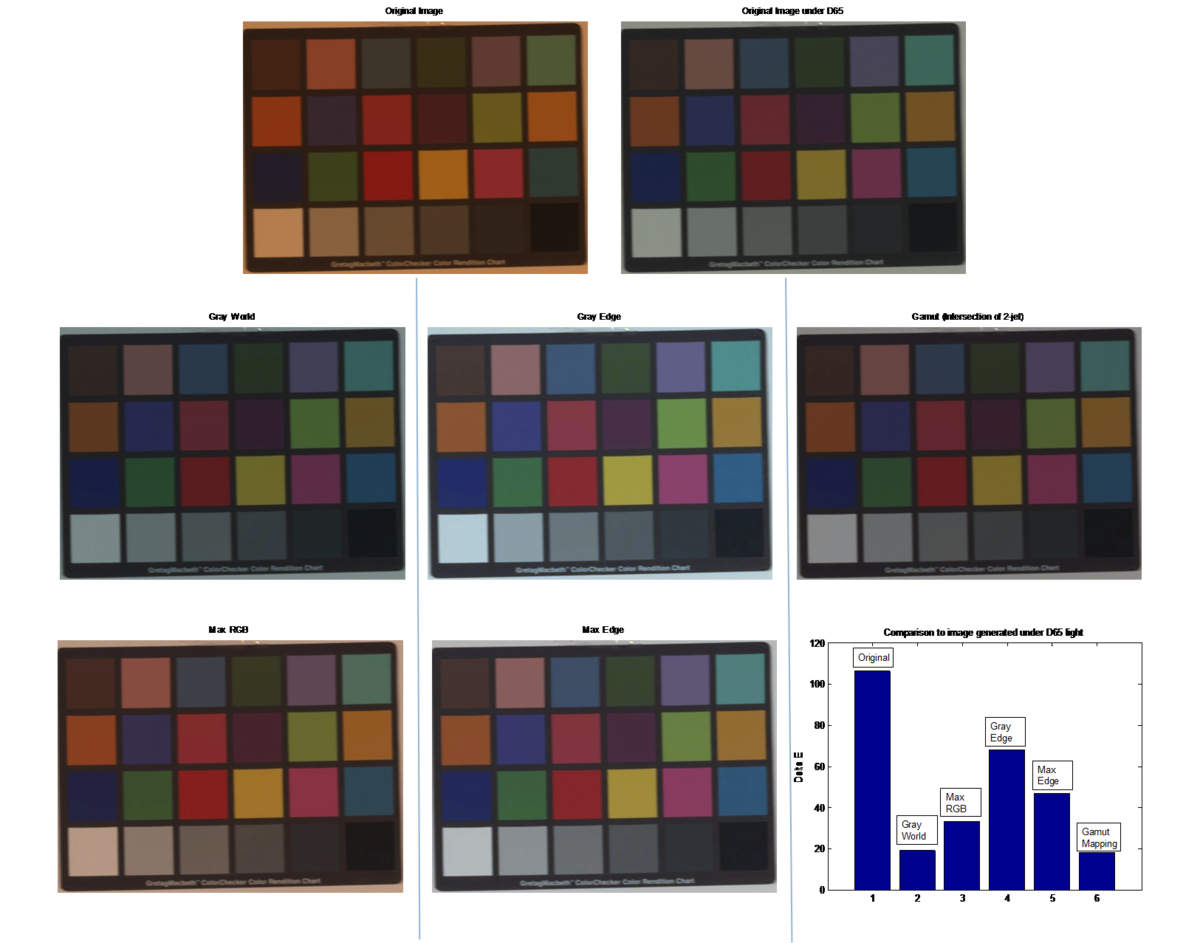
Image set 2
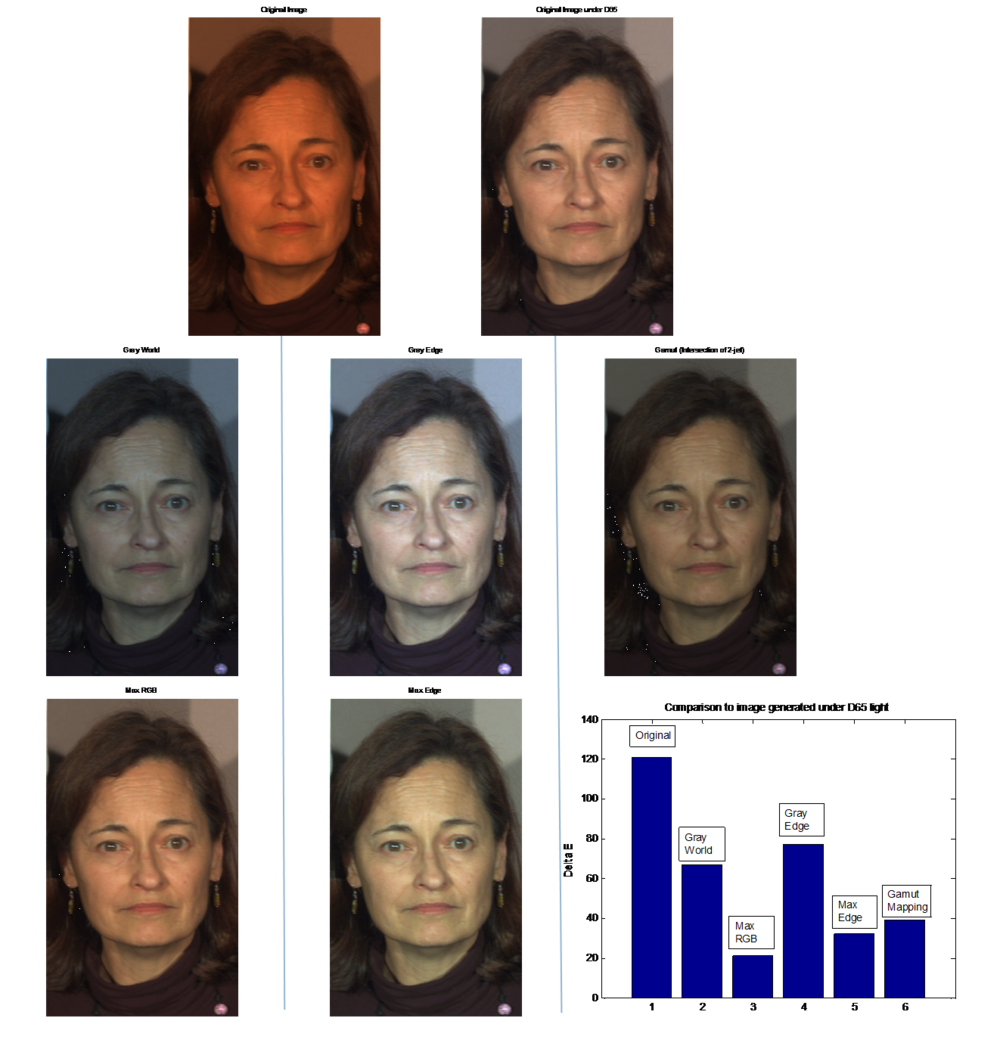
Image set 3
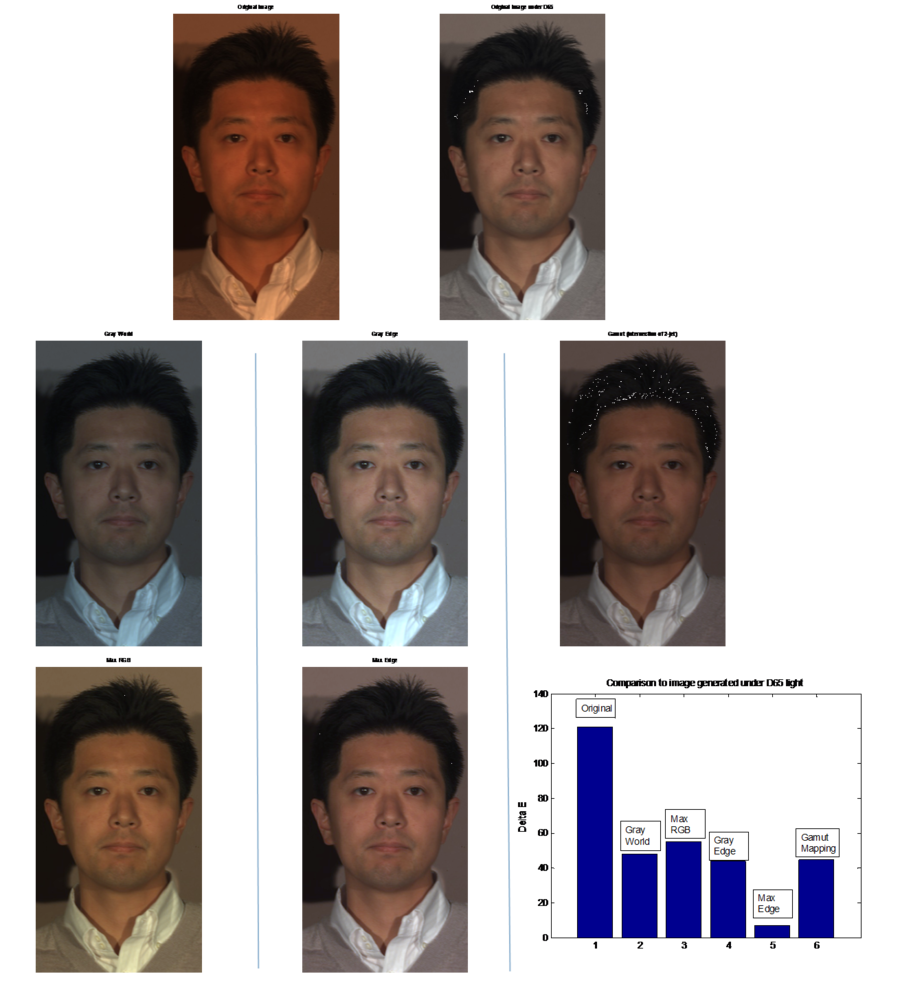
Image set 4

Conclusions
We see from this sample of results that these algorithms are highly dependent on the input scene. Even a small area in the scene can widely affect the performance of these methods. We would need to test on a larger variety of illuminants to reach more conclusive results, especially since the edge based algorithms seem to work better for outdoor images.
We also conclude that simple algorithms can achieve similar performance to more complex algorithms. While the gamut mapping method referenced in this project needs heavy computation (calibration over a set of canonical gamuts and needs to use convex optimization), the other methods described can be run in real time without having to use too much special hardware. For future work, it may be useful to see how robust a combination of these methods would be.
[1] A. Gijsenij, T. Gevers, J. van de Weijer. "Generalized Gamut Mapping using Image Derivative Structures for Color Constancy.
[2] J. van de Weijer, T. Gevers, A. Gijsenij. "Edge-Based Color Constancy"