Alex

Retinotopy/Attenotopy

This project is about mapping field maps in high level visual areas. Over the last years it has been shown that with a few modifications to the classic retinotopy paradigm and better processing techniques, more maps can be consistently found in more areas in addition to occipital cortex. One version of these paradigm modifications, is making the subject covertly attend to the rotating wedge by having a target detection task, while the subject maintains fixation. This is method is appropriately named attenotopy. Furthermore, evidence shows that there are attention processes occurring in parietal cortex. By having an embedded attention task in the classic retinotopy task, we will be able to map visual fields in parietal cortex in addition to all the other occipital cortex maps.

Background

Many cortical areas have a one to one mapping between visual field and cortical location (Bressler and Silver 2010). A natural way to explore this is to have a stimulus that traverses the visual field in some fashion, and then do some type of correlation analysis between visual field location and brain activity. Engel et al. (1993,1994,1997) were one of the first experimenters to develop a continuos stimuli covers all of the visual space. They showed that by using a traveling wave analysis for a rotating wedge and moving concentric circles stimuli, the visual field maps could be produced in occipital cortex. Figure 1, taken from Wandell et al. 2007 illustrates this method.

Figure 1

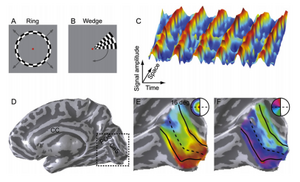
Figure 1: Traveling Wave Method for creating retinotopic field maps in occipital cortex. Referred to Wandell et al. 2007 for more details.

Several other cortical areas have been mapped with fMRI including: V1,V2,V3,V4, V3A, V3B, V6, V7 or IPS0, IPS1, IPS2, IPS3 , IPS4, V01, V02, PHC1,PHC2 among many others (Silver and Kastner 2009). Not that some of these areas extend beyond what was classically thought to be visual cortex. Visual maps in IPS(0-4) lie on the posterior part of parietal cortex. This particular region has been associated with cognitive processes such as attention and memory (Silver and Kastner 2009, see also Bressler and Silver 2010). Specifically, it is now widely accepted that allocation of attention while doing a retinotopic experiment increases the ability to produce field maps (Wandell and Winawer 2011, Bressler and Silver 2010). To this effect, Bressler and Silver made a quantitative study in order to analyze the gain in terms of SNR of this effect. This project uses the same stimuli as the Bressler study and produces similar maps.

Methods

As mentioned before the stimuli used was as in Bressler and Silver 2010, Figure 2. A flickering checkerboard rotating wedge traverses the visual field in clockwise fashion. The wedge is 45 degrees wide, and extends 0.5 degrees to 10.9 degrees from a central fixation. The wedge rotates 22.5 deg locked to the scanner's TR at 2.13s. It takes the wedge 34.13 seconds to complete a cycle and there are 8 cycles that go into the analysis. A target appears with 50% probability inside the wedge. The subject is instructed to respond when a target appears, while maintaining fixation. Refer to Bressler and Silver 2010 for more details.

Figure 2

Figure 2: Rotating Wedge with an embedded target detection task.

For this project only one subject was analyzed. mrVista was used for data preprocessing and analysis. Traditional retinotopy analyzes were used, i.e. the coherence between the frequency produced by a stimulus cycle of 34.13s and the average fMRI time series for each voxel was calculated (Engel et al. 1994). The resulting maps are transformed into an inflated 3D cortical view.

You can use subsections if you like. Below is an example of a retinotopic map. Or, to be precise, below will be an example of a retinotopic map once the image is uploaded. To add an image, simply put text like this inside double brackets 'MyFile.jpg | My figure caption'. When you save this text and click on the link, the wiki will ask you for the figure.

Below is another example of a reinotopic map in a different subject.
Figure 2

Once you upload the images, they look like this. Note that you can control many features of the images, like whether to show a thumbnail, and the display resolution.

Figure 3

MNI space

MNI is an abbreviation for Montreal Neurological Institute.

Methods

Measuring retinotopic maps

Retinotopic maps were obtained in 5 subjects using Population Receptive Field mapping methods Dumoulin and Wandell (2008). These data were collected for another research project in the Wandell lab. We re-analyzed the data for this project, as described below.

Subjects

Subjects were 5 healthy volunteers.

MR acquisition

Data were obtained on a GE scanner. Et cetera.

MR Analysis

The MR data was analyzed using mrVista software tools.

Pre-processing

All data were slice-time corrected, motion corrected, and repeated scans were averaged together to create a single average scan for each subject. Et cetera.

PRF model fits

PRF models were fit with a 2-gaussian model.

MNI space

After a pRF model was solved for each subject, the model was trasnformed into MNI template space. This was done by first aligning the high resolution t1-weighted anatomical scan from each subject to an MNI template. Since the pRF model was coregistered to the t1-anatomical scan, the same alignment matrix could then be applied to the pRF model.
Once each pRF model was aligned to MNI space, 4 model parameters - x, y, sigma, and r^2 - were averaged across each of the 6 subjects in each voxel.

Et cetera.

Results - What you found

Retinotopic models in native space

Some text. Some analysis. Some figures.

Retinotopic models in individual subjects transformed into MNI space

Some text. Some analysis. Some figures.

Retinotopic models in group-averaged data on the MNI template brain

Some text. Some analysis. Some figures. Maybe some equations.

Equations

If you want to use equations, you can use the same formats that are use on wikipedia.
See wikimedia help on formulas for help.
This example of equation use is copied and pasted from wikipedia's article on the DFT.

The sequence of N complex numbers x₀, ..., x_N−1 is transformed into the sequence of N complex numbers X₀, ..., X_N−1 by the DFT according to the formula:

$X_{k}=\sum _{n=0}^{N-1}x_{n}e^{-{\frac {2\pi i}{N}}kn}\quad \quad k=0,\dots ,N-1$

where i is the imaginary unit and $e^{\frac {2\pi i}{N}}$ is a primitive N'th root of unity. (This expression can also be written in terms of a DFT matrix; when scaled appropriately it becomes a unitary matrix and the X_k can thus be viewed as coefficients of x in an orthonormal basis.)

The transform is sometimes denoted by the symbol ${\mathcal {F}}$, as in $\mathbf {X} ={\mathcal {F}}\left\{\mathbf {x} \right\}$ or ${\mathcal {F}}\left(\mathbf {x} \right)$ or ${\mathcal {F}}\mathbf {x}$.

The inverse discrete Fourier transform (IDFT) is given by

$x_{n}={\frac {1}{N}}\sum _{k=0}^{N-1}X_{k}e^{{\frac {2\pi i}{N}}kn}\quad \quad n=0,\dots ,N-1.$

Retinotopic models in group-averaged data projected back into native space

Some text. Some analysis. Some figures.

Conclusions

Here is where you say what your results mean.

References - Resources and related work

References

Software

Appendix I - Code and Data

Code

File:CodeFile.zip

Data

zip file with my data

Appendix II - Work partition (if a group project)

Brian and Bob gave the lectures. Jon mucked around on the wiki.