QuachFu: Difference between revisions
imported>Projects221 No edit summary |
imported>Projects221 No edit summary |
||
| Line 100: | Line 100: | ||
== Uncompressed Images == | == Uncompressed Images == | ||
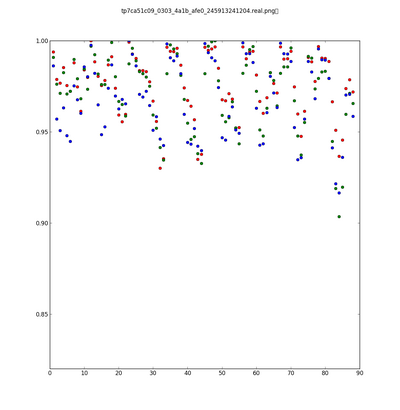
[[File:RealPlot.png | [[File:RealPlot.png |400px|Figure 4: Normalized Similarity Measure for Original Image]] [[File:FakePlot.png|400px|Figure 5: Normalized Similarity Measure for Tampered Image]] | ||
Revision as of 09:37, 19 March 2013
Back to Psych 221 Projects 2013
Background
Digital Image Forgery
Digital cameras have long since replaced traditional cameras as the dominant form of photography. Their practicality coupled with the combination of low cost and high performance have made them extremely popular. Additionally, with the advent of the camera phone, nearly every person now has a camera on them at all times. This has led to an explosion of images of nearly anything that can be easily found on the internet. Combined with very power photo editing software such as Photoshop, the amount of forged images has also dramatically increased. Images of a subject or event can longer be blindly taken at face value since it has become so easy to forge them. Because of this, it has become increasingly important to be able to discern legitimate images from forged ones. It is possible to leverage how digital camera sensors record images to determine if they have been altered and post-processed.
Digital Camera Image Sensors
Each pixel in a color digital image consists of three different values: its red, green, and blue intensity. Therefore, the entire image can be thought to have three separate channels--one for each color. However, each of the CMOS imaging chip's photosensors, which will record the light in the scene for a single pixel, can only detect light intensity without wavelength information. Therefore, they are unable to separate color information and record a separate value for each channel. To work around this limitation, image sensors typically employ a color filter array (CFA), which is a mosaic of tiny color filters placed on top of the image sensor, so that for each individual pixel, only a single band of light will pass through it and be recorded onto the pixel. Figure 1 depicts a common CFA known as a Bayer array, which employs a pattern of red, blue, and green color filters.

CFA Interpolation
In order to construct a complete image with RGB values for every pixel, we must estimate the two missing color values at each pixel by interpolating the values of neighboring pixels. There are numerous interpolation algorithms that can be used, which can vary between the make and model of the camera.
Camera Forensics using CFA Interpolation
A technique used to determine if an image has been altered leverages the properties of CFA interpolation. In an undoctored image, there will be a strong correlation between the estimated color values and its values of its neighbors. However, if an image has been digitally altered, these correlations will likely be destroyed. Even if an image has been created by combining two unaltered images together, the interpolation pattern will not remain the same across the subimage boundaries. Therefore, by measuring the strength of the periodic pattern of interpolated pixels in an image, we can tell if an image has been doctored or not.
Expectation Maximization
Given an image, we do not know both the exact parameters of the interpolation algorithm, nor which pixels are being estimated. Since we have two unknowns, we need to use an expectation/maximization (EM) algorithm to estimate both unknowns at the same time. We assume a simple linear model for the interpolation algorithm, which may not be exact, but is simple and will give a decent approximation of more complex CFA algorithms. We also assume each color channel is interpolated independently. Therefore, we run the EM algorithm for a single color channel at a time. Lastly, we assume each pixel belongs to one of two models: 1 if the pixel is estimated from its neighbors, and 2 if it is not.
E-Step
In the expectation step, we estimate the probability of each pixel belonging to a particular model. We can estimate the probability of a sample belonging to Model 1 using Bayes' Rule:
Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. TeX parse error: Undefined control sequence \emph"): {\displaystyle \Pr\{{\emph {f(x,y)}}\in M_{1}\mid {\emph {f(x,y)}}\}={\frac {\Pr\{{\emph {f(x,y)}}\mid {\emph {f(x,y)}}\in M_{1}\}\Pr\{{\emph {f(x,y)}}\in M_{1}\}}{\sum _{i=1}^{2}{\Pr\{{\emph {f(x,y)}}\mid {\emph {f(x,y)}}\in M_{1}\}\Pr\{{\emph {f(x,y)}}\in M_{1}\}}}}}
where Failed to parse (Conversion error. Server ("https://wikimedia.org/api/rest_") reported: "Cannot get mml. TeX parse error: Undefined control sequence \emph"): {\displaystyle \Pr\{{\emph {f(x,y)}}\mid {\emph {f(x,y)}}\in M_{1}\}\}={\frac {1}{\sigma {\sqrt {2\pi }}}}exp(-{\frac {[{\emph {f(x,y)}}-\sum _{u,v=-N}^{N}{\alpha _{u,v}f(x+u,y+v)}]^{2}}{2\sigma ^{2}}})}
The initial values of the variance is the inverse of the range of f(x,y). Random values between 0 and 1 are chosen to initialize all the coefficients.
M-Step
The M-step minimizes the quadratic error function
To minimize this equation, the partial derivative with respect to each is taken to form the equation:
When all partial derivatives of are taken, then there will be unknowns and equations (because is always 0). These linear set of equations and unknowns can be then solved using linear algebra to find new . This was done using Matlab's linsolve() function. Each coefficient for the left hand side of the equation was put into its respective place in a matrix and a vector was created for the right hand side of the matrix. Matlab's linsolve() function could then take the matrix representing the coefficients of each and the vector for values on the right hand side of the equation, and solve for all unknowns. The EM algorithm repeats until it converges. Convergence would be if the difference between the last iteration and the current iteration is less than .
A new variance estimate is also done in the M-step with the equation:
Probability Map
Here we display the probability map, which lists of the probability of each pixel being interpolated, as an image. The periodicity is not visible, likely due to the small size of each pixel.

2D FFT
If we take the two dimensional FFT of the probability map and plot it, then we can more clearly see the periodic patterns which manifests itself as peaks in the graph. In the figure below, the probability map is up-sampled by a factor of two in order to push the peaks towards the center for visibility reasons. The resulting FFT data is also shifted to move the zero peak to the center, as well as having the log() function and gamma correction applied to it to make the peaks more distinct. The peaks in the center of each quadrant represent the periodic pattern of the interpolated pixels.

Similarity Measure
A synthetically generated probability map was produced with the following definition for each color channel:
We assume a Bayer CFA was used to generate the images so in order to produce one in Matlab the synthetically generated maps followed this pattern:
, , , and
We run a sliding 128px by 128px window with 64px stride (50% overlap) over the probability map of the image and synthetically generated probability map. We then take the 2D FFT of the subimage contained in the window and run the similarity measure calculation against the corresponding subimage of the synthetically generated probability map.
The similarity measure is defined as
and are the Fourier transforms of the probability map and synthetic probability map of the green channel. Similar calculations are done for the red and blue channels.
Thresholding
Threshold values were determined empirically from test image sets. An image is classified as being fake if all three color channels fall below their respective threshold value for any one subimage.
Results
Uncompressed Images
JPEG Images
Equations
If you want to use equations, you can use the same formats that are use on wikipedia.
See wikimedia help on formulas for help.
This example of equation use is copied and pasted from wikipedia's article on the DFT.
The sequence of N complex numbers x0, ..., xN−1 is transformed into the sequence of N complex numbers X0, ..., XN−1 by the DFT according to the formula:
where i is the imaginary unit and is a primitive N'th root of unity. (This expression can also be written in terms of a DFT matrix; when scaled appropriately it becomes a unitary matrix and the Xk can thus be viewed as coefficients of x in an orthonormal basis.)
The transform is sometimes denoted by the symbol , as in or or .
The inverse discrete Fourier transform (IDFT) is given by
Conclusions
Here is where you say what your results mean.
[1] Farid, H. Exposing Digital Forgeries in Color Filter Array Interpolated Images. Signal Processing, IEEE Transactions. Vol. 53, Issue 10. October 2005.
Appendix I - Code and Data
Code
Data
Appendix II - Work partition (if a group project)
Brian and Bob gave the lectures. Jon mucked around on the wiki.