WooLee

Back to Psych 221 Projects 2013

Background

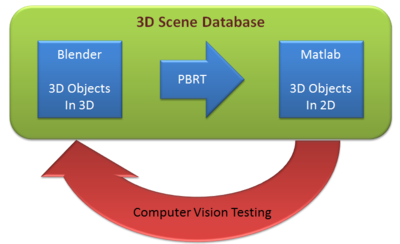
It is no wonder that vision is one of the most important parts in our lives. Besides, due to the tremendous improvements in technology, research on 3D vision has become hot topic. 3D reconstruction is interesting in a way that we could realize a 3D image by just looking at a 2D image. In this project, we provide some techniques for developing scene models that could be used in analysis in ISET. We build the scene using Blender and export it to PBRT files. Then, in Matlab, we run the ISET to analyze the scene converted. We also attempted to do 3D reconstruction, demonstrating a possible way of using scenes for computer vision testing.

Figure 1 Overview

Figure 2

Once you upload the images, they look like this. Note that you can control many features of the images, like whether to show a thumbnail, and the display resolution.

Figure 3

Blender

Blender allows us to design 3D objects in 3D space. It has various features, such as modeling, texturing, lighting, animation and video post-processing functionality. Also, it is highly compatible with other files so that we can make use of other 3D files to edit them. The figure below shows basic Blender interfaces.

Figure 2

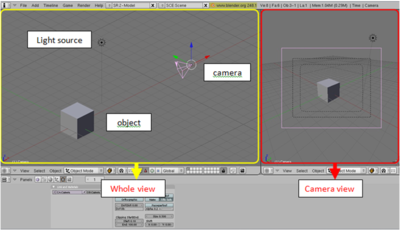
Take a cube as an example as shown fig.x. There is an object, which is a cube in this example, light source, and camera. On the left side of the figure.x, it shows whole scene that we created, on the right side, it shows the scene which is viewed through the camera. We can control the parameters and the properties of those; - object : edit geometry, size of the object, control reflectance such as diffuse, specular - light source : set light source as you would like to use such as D65 - camera : viewing position, choose lens

PBRT

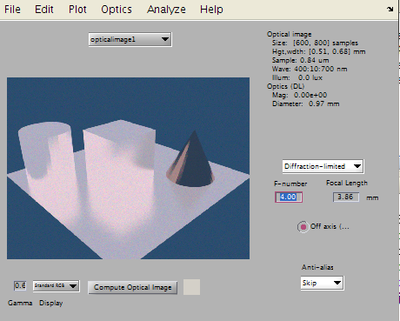
PBRT stands for Physically Based Rendering Tool, and it is a render for graphics. It does not have any specific interface like Blender. Of various functions, transferring a 3D image data of an object to a 2D image data is the function that we are looking for. PBRT is a powerful that it can store the 2D data as if we take a picture of a 3D object. It takes point of view, reflectance, shades, etc. into account when converting. Below shows the converted 2D picture from 3D objects.

Methods

Using Blender to Create Scenes

In our project, Blender is used for creating scene. In our case, we must use the version 2.48a. There are few steps to do this.

1) import the file

Import the file which is filename.dae.

2) texturing

To make texture on the object, texture image is needed, and it should be converted to .tga format. Then we put the texture image on the object. Also, we can apply the material to the object using texture menu shown in the figure.

Figure

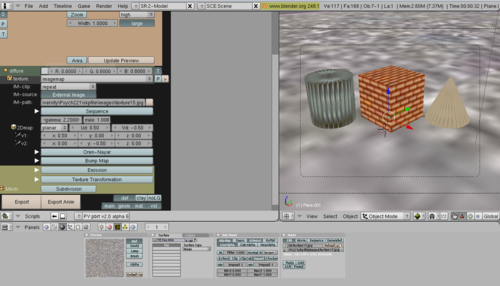
3) control reflectance

We are able to control reflectance, light source as well. In the case of reflectance, it is allowed to apply diffuse and specular reflectance on the object.

Figure

4) export to pbrt

Finally, the scene has been created by exporting the image to pbrt using exporter. Go to render menu, and click the export to pbrt.

Here are some examples of 3D objects created via Blender.

Figure

Figure

Figure

Using PBRT to create 3D scene

1) Set up

First of all, we need to initialize ISET and configure some files to make PBRT work. Go to the corresponding ISET directory in Matlab and type:
>> isetPath(pwd)
>> ISET
We have used scene3Dmatlab directory (downloadable). In that directory type:
>> addpath(genpath(pwd))
Now, we are ready to use PBRT.

2) PBRT files

From the exporter in Blender, we achieve several files. Those are default.pbrt, default-geom.pbrt, and default-mat.pbrt (default-vol.pbrt is not used, and the name default can be changed). Brief descriptions are below:
- default.pbrt : includes camera lens information, sampling pixels
- default-geom.pbrt : includes the geometry of the objects
- default-mat.pbrt : includes the information for the material such as texture
Some files, if necessary, need to be changed, such as file paths for texture and minor settings (number of sampling pixels, camera position, etc).

3) Run PBRT

We can execute PBRT in a command line, but we prefer to use Matlab because we could make coding neat and use features in Matlab in order to analyze PBRT files. The following is the code we used:

chdir(fullfile(s3dRootPath, 'scripts', 'pbrtFiles'));
unix([fullfile(pbrtHome, '/src/bin/pbrt ') 'default.pbrt']); # generate PBRT to make images
oi = pbrt2oi('output.dat');
vcAddAndSelectObject(oi);
oiWindow;
m = oiGet(oi, 'mean illuminance')

We can open this output with ISET. Other detailed codes are attached in the references With this image files we can now consider doing some computer vision testing.

Computer Vision Testing: 3D depth reconstruction

1) Ideas for 3D depth reconstruction

We decide to try simple 3D reconstruction. We will use 2 images: one is original image, the other is shifted image of the original one. By using two images mentioned above, we can get a depth that that could be used in 3D reconstruction. From the 2D images and for each certain portion we check how that portion is close to the portions in the other image.

Method 1: Autocorrelation

3D reconstruction can be done by using the concept of autocorrelation. The highest value of the autocorrelation is always the multiplication of itself, meaning the same image portion in our case. We fix the position of the portion in the original figure and move that in the second figure to compute the autocorrelation. For this computation we also include normalized constant to take weight into account. Once the highest value of the autocorrelation is found we select that that position of the second image corresponds to that of the first image.

Method 2: Subtraction

Another approach is we subtract the image portion of original to that of the other. And then sum all the values computed. Other than this we do the same procedure: move the portion of the second image and compute the subtraction (also normalization is included here). In this case, however, the lowest values will let us know the position of the second image that corresponds to that of the first image.

Generate 3D depth Map

We can measure the distance of the positions. If an object is further from the camera views, the distance would be short. If an object is close to the camera views, the distance would be long. From this we can generate depth-map plot, giving high values to close objects and low values to distant objects.

2) Generating two 2D camera view images

In order to do 3D reconstruction. We need two images, and the viewpoints of them need to share at least one axis and perpendicular to the viewing direction. After exporting from Blender to PBRT, we can create another PBRT file viewing from another perspective by adjusting LookAt in default.pbrt. Utilizing the concept of linear algebra, we can deduce the points for the second camera. This way we would avoid uncertain error made in Blender because the computation of such point would be much more accurate than moving a camera. The following figure shows the vector of the camera.

Figure

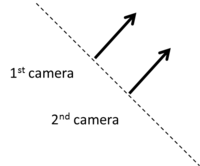
We know the two points consisting of the direction vector of the first camera. Using those points, we can get the vector points for the second camera.

(결과에 붙여넣기)The figure on the right hand side below shows the PBRT-converted 3D scene from 3D objects in the figure on the left hand.

Results - What you found

Retinotopic models in native space

Some text. Some analysis. Some figures.

Retinotopic models in individual subjects transformed into MNI space

Some text. Some analysis. Some figures.

Retinotopic models in group-averaged data on the MNI template brain

Some text. Some analysis. Some figures. Maybe some equations.

Equations

If you want to use equations, you can use the same formats that are use on wikipedia.
See wikimedia help on formulas for help.
This example of equation use is copied and pasted from wikipedia's article on the DFT.

The sequence of N complex numbers x₀, ..., x_N−1 is transformed into the sequence of N complex numbers X₀, ..., X_N−1 by the DFT according to the formula:

$X_{k}=\sum _{n=0}^{N-1}x_{n}e^{-{\frac {2\pi i}{N}}kn}\quad \quad k=0,\dots ,N-1$

where i is the imaginary unit and $e^{\frac {2\pi i}{N}}$ is a primitive N'th root of unity. (This expression can also be written in terms of a DFT matrix; when scaled appropriately it becomes a unitary matrix and the X_k can thus be viewed as coefficients of x in an orthonormal basis.)

The transform is sometimes denoted by the symbol ${\mathcal {F}}$, as in $\mathbf {X} ={\mathcal {F}}\left\{\mathbf {x} \right\}$ or ${\mathcal {F}}\left(\mathbf {x} \right)$ or ${\mathcal {F}}\mathbf {x}$.

The inverse discrete Fourier transform (IDFT) is given by

$x_{n}={\frac {1}{N}}\sum _{k=0}^{N-1}X_{k}e^{{\frac {2\pi i}{N}}kn}\quad \quad n=0,\dots ,N-1.$

Retinotopic models in group-averaged data projected back into native space

Some text. Some analysis. Some figures.

Conclusions

Here is where you say what your results mean.

References - Resources and related work

References

Software

Appendix I - Code and Data

Code

File:CodeFile.zip

Data

zip file with my data

Appendix II - Work partition (if a group project)

Brian and Bob gave the lectures. Jon mucked around on the wiki.