Brittany: Difference between revisions
imported>Psych204B No edit summary |
imported>Psych204B No edit summary |
||
| Line 45: | Line 45: | ||
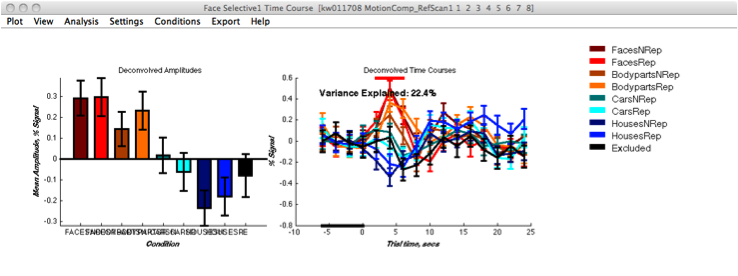
[[File:FS1 | [[File:FS1 Timecourse2.png | Figure 5]] | ||
= Results - What you found = | = Results - What you found = | ||
Revision as of 06:14, 15 March 2012
The Relationship between fMRI adaptation and category selectivity
This project investigates the link between adaptation and areas of the cortex linked to face recognition and limb recognition using an event related design.
Background
fMRI Adaptation is a phenomena that takes place in higher order cortical areas in which the BOLD response signal decreases in response to repeated identical visual stimuli. Adaptation has been shown to occur in higher order visual areas but not early visual areas such as V1 [1]. This study investigates the relationship between object selectivity and fMRI adapation. More specifically, it will examine face selective areas as well as body part selective areas with regards to adaptation. Furthermore, it will look at the differences between adaptation within the ROIs of those two specific categories as well as the similarities in adaptation across various anatomical brain areas.
Methods
Pre-processed data was used from the lab of Kalanit Grill-Spector from the parts of an experiment outlined below [2].
Subjects
The data from the right hemisphere of one subject, a male in his late 20s, was analyzed.
MR acquisition
The subject participated in two experiments, an event related design followed by a block design localizer scan. The first, event related design, consisted of 8 runs of 156 trials lasting for 2 seconds each. Each trial consisted of the presentation of an image of either a face, limb, car, or house for 1000ms followed by a 1000ms blank. Within each run, only two of the images were repeated six times, the rest not repeated at all. None of the images were repeated across scans.
The second experiment was a block design used to identify category selective areas within the ventral stream. Blocks were 12 seconds long with a 750ms stimulus presentation period followed by a 250 ms blank period. Each run consisted of 32 blocks, 4 blocks for each category (faces, limbs, flowers, cars, guitars, houses, and scrambled) as well as four blank blocks.
12 slices were acquired at a resolution of 1.5 x 1.5 x 3mm per voxel and a TR of 1000 ms.
MR Analysis
As mentioned above, the data I analyzed was pre-processed. That high resolution MR data was was then analyzed using mrVista software tools.
ROIs
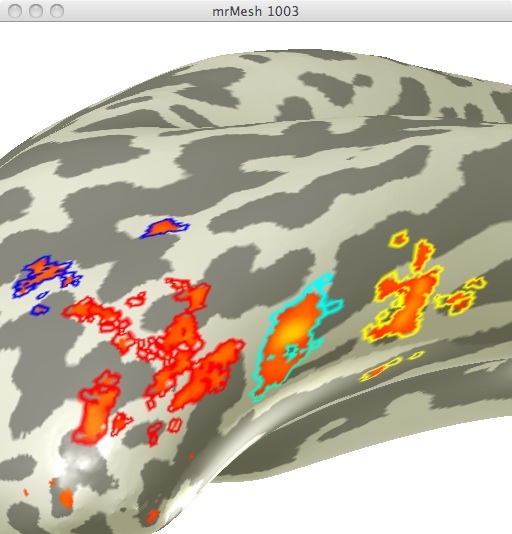
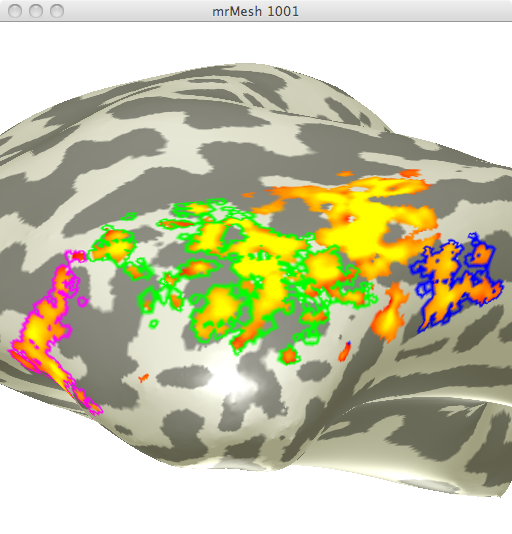
Using the localizer data from the second experiment, I created ROIs specific for areas selective for faces and areas selective for limbs. I chose the 4 different face selective areas seen in figure 1.
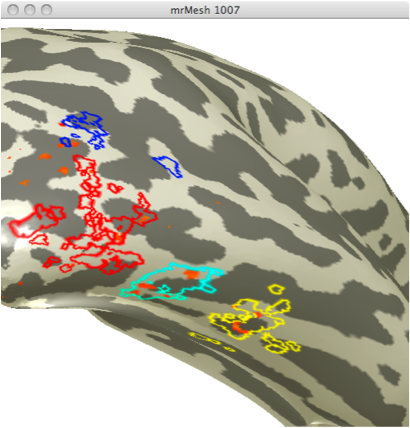
Using the localizer data for limb selective regions from the same experiment I selected 3 limb selective ROIs (See figure 2). I chose these 3 ROIs in order to obtain data from one ROI in 3 differing anatomical regions.
These ROIs were then uploaded onto their respective adaptation maps obtained from the first experiment. Face Selective adaptation map(figure 3) and Limb selective adaptation map (figure 4).
FIGURE 3 FIGURE 4
Results - What you found
Retinotopic models in native space
Some text. Some analysis. Some figures.
Retinotopic models in individual subjects transformed into MNI space
Some text. Some analysis. Some figures.
Retinotopic models in group-averaged data on the MNI template brain
Some text. Some analysis. Some figures. Maybe some equations.
Equations
If you want to use equations, you can use the same formats that are use on wikipedia.
See wikimedia help on formulas for help.
This example of equation use is copied and pasted from wikipedia's article on the DFT.
The sequence of N complex numbers x0, ..., xN−1 is transformed into the sequence of N complex numbers X0, ..., XN−1 by the DFT according to the formula:
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle X_k = \sum_{n=0}^{N-1} x_n e^{-\frac{2 \pi i}{N} k n} \quad \quad k = 0, \dots, N-1}
where i is the imaginary unit and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle e^{\frac{2 \pi i}{N}}} is a primitive N'th root of unity. (This expression can also be written in terms of a DFT matrix; when scaled appropriately it becomes a unitary matrix and the Xk can thus be viewed as coefficients of x in an orthonormal basis.)
The transform is sometimes denoted by the symbol Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{F}} , as in Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{X} = \mathcal{F} \left \{ \mathbf{x} \right \} } or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{F} \left ( \mathbf{x} \right )} or Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathcal{F} \mathbf{x}} .
The inverse discrete Fourier transform (IDFT) is given by
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle x_n = \frac{1}{N} \sum_{k=0}^{N-1} X_k e^{\frac{2\pi i}{N} k n} \quad \quad n = 0,\dots,N-1.}
Retinotopic models in group-averaged data projected back into native space
Some text. Some analysis. Some figures.
Conclusions
Here is where you say what your results mean.
References
Software