Okkeun Lee
Introduction
Contrast sensitivity function (CSF) is a subjective measurement of an ability of the visual system to detect a low contrast pattern stimuli. The stimuli considered usually are vertical sinusoidal Gabor patches of decreasing shades of black to grey. This use of sine wave gratings was first introduced in vision by Schade (1956) [1] and was subsequently used by early investigators to measure basic visual sensitivity (Westheimer, 1960) [2]. The resulting measurement is used to validate the representation of the eyes' visual performance as it complements the visual acuity. CSF is synonyms with an audiogram where a person’s highest detectable pitch is measured and well as the ability to hear all lower pitches.[3]
The CSF measurements are usually acquired with small patches of sinusoidal grating designed to fall within few central degrees of the visual field. It is well known that the CSF decreases as one measures contrast sensitivity at increasingly peripheral locations in the visual field. The reasons for such decreased CSF is attributed to a number of neural factors. [4] The human eye is structured such that the distribution of the cone mosaic falls off rapidly as a function of visual eccentricity, so that there are fewer sensors available to detect and encode the incoming stimuli. Towards the periphery the amount of retinal ganglion cells’ density falls as well. This structure of the cones is also a key factor in deciding the CSF. In particular, for this project, we make an effort to explore the role of inference engines in shaping the CSF.
Background
The human visual system’s CSF or the modulation transfer function (MTF) fundamentally characterises eye’s spatial frequency response and thus, one may think of it as a bandpass filter. This bandpass nature, however, is determined by a variety of factors such as the front-end optics, cone distribution geometry and the neural mechanism that is responsible for this interpretation which is typically inferred using the machine learning techniques such as the KNN and SVM. [5]
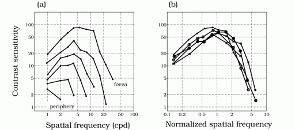
The methods of CSF measurement usually employ sine-wave gratings of a fixed frequency. By varying the frequency, a set of stimuli are constructed. The response of the eye to these stimuli are then determined. This procedure is repeated for a large number of grating frequencies. The resulting curve is called the contrast sensitivity function and is illustrated in Fig. 1. [6]
From the measurements, contrast sensitivity score is determined such that it is equal to (1/threshold) for the given spatial form. The contrast sensitivity scores obtained for each of the sine-wave gratings examined are then plotted as a function of target spatial frequency yielding the contrast sensitivity function (CSF). [7] Some typical CSF's are depicted in Figure 1 below shows the typical inverted-U shape of the CSF on logarithmic axes.
The Robson JG and Graham N [8] have demonstrated that the CSF attains its maximum while using foveal vision as indicated in In Fig 2. They observed that the CSF reduces with increasing retinal eccentricity. Further, the CSF declines with eccentricity is greater for higher spatial frequencies but more gradual for lower spatial frequencies. [9]
Methods
In order to determine the CSF for various spatial frequency, we have used the readily available tool from the MATALB called The Image System Engineering Toolbox for Biology (ISETBio). The ISETBio is sold by Imageval Consulting, LLC and available as an open source project. The toolbox is primarily used to design image sensors as well as for modeling image formation in biological systems and thus used widely for commercial and research purposes.
We have used ISETBio first to simulate the cone photoreceptor absorptions, which is the first stage processing in human vision and thus the CSF to some extent is determined by the photoreceptors. One of the factors that still remains unclear is the relation between size of the photoreceptors and the CSF as they are small in the fovea and much larger in the periphery . In order to include the cone mosaic distribution factors into account, we generated two portions of the retina- the center of the fovea, and slightly to the periphery using the “coneMosaic” method in ISETBio. We computed the CSF for six spatial frequencies from 1 to 1.5 in log space. We also varied the integration time in the retina as a factor in order to know how the integration factor affects the CSF. For each of the frequency, we generated a Gabor patch stimulus and obtained the visual response using the toolbox. The stimulus responses between the null and the Gabor patch stimulus was discriminated by using the inference engines from machine learning. In particular, we were interested to compare the performance of both the support vector machines (SVM) and k-nearest neighbors (kNN) algorithm in terms of their role in inferring the CSF.
SVM is a supervised learning method developed at AT&T Bell Laboratories by Vapnik with colleagues (Boser et al., 1992, Guyon et al., 1993, Vapnik et al., 1997). The way we used the SVM in our experiment is as follows: we marked the responses that belong to stimuli and null stimuli categories as one or zero, respectively. We then trained the SVM using the training samples and tested the model with the test set. We computed the percentage of correct detection of stimuli by the SVM and compare it against the given threshold to see if for the set of front-end optic parameters and the cone mosaics the contrast change is detected. We repeated this for various spatial frequencies and thus obtained the CSF curves.
Results
Conclusions
Limitations and Future Work
Reference
[1] Otto H. Schade, Optical and Photoelectric Analog of the Eye, J. Opt. Soc. Am. 46, 721-739 (1956)
[2] Westheimer, G. (1960). Modulation thresholds for sinusoidal light distributions on the retina. Journal of Physiology, 152, 67-74
[3] http://www.ssc.education.ed.ac.uk/resources/vi&multi/VIvideo/cntrstsn.html
[4] Jennings, J. A., & Charman, W. N. (1981). Off-axis image quality in the human eye. Vision Research, 21(4), 445–455.
[5] Nicolas P. Cottaris, Brian A. Wandell, Fred Rieke, David H. Brainard; A computational observer model of spatial contrast sensitivity: Effects of photocurrent encoding, fixational eye movements, and inference engine. Journal of Vision 2020;20(7):17
[6] https://foundationsofvision.stanford.edu/chapter-7-pattern-sensitivity/
[7] http://usd-apps.usd.edu/coglab/CSFIntro.html
[8] Robson JG, Graham N. Probability summation and regional variation in contrast sensitivity across the visual field. Vision Res. 1981;21:409–18.
[9] Skalicky S.E. (2016) Contrast Sensitivity. In: Ocular and Visual Physiology. Springer, Singapore. https://doi.org/10.1007/978-981-287-846-5_20