Medical imaging: Simulations of human oral mucosa tissue fluorescence

Introduction

Autofluorescence spectroscopy has emerged as a promising noninvasive technique since it can diagnose oral neoplasia with sensitivity and specificity []. Clinical data indicate that neoplastic progression in the oral cavity is associated with a number of characteristic spectral changes, which come from the altered optical properties of both the superficial epithelium and the underlying stroma []. These changes include an increase in epithelial cell scattering, increased stromal hemoglobin content, and decreased structural protein fluorescence within the stroma. Therefore, the interpretation of fluorescence spectra collected in vivo in terms of these biochemical and morphologic changes is crucial. To understand better on how these optical parameters can alter the intensity and shape of the fluorescent spectra, and thereby guide the spectra interpretation to physiological changes, we developed a Monte Carlo model using MCMaltab with site-specific input to simulate the fluorescence spectra on normal, and damaged oral sites. Our goal in developing this model was to provide a computational tool to study how the morphological characteristics of the tissue affect the final fluorescent spectra.

Methods

In MCMatlab simulation, we need to determine 2 components of model settings: 1. Geometry model; 2 Media property model; to construct our oral tissue model.

Geometry Model

Geometry model in MCMatlab is used to build a 3D model object with multiple voxels where the light is propagating through, which includes specifying below key inputs:

- Dimensions of the model cuboid: By specifying the side lengths Lx, Ly, Lz.

- Number of bins along each axis of the model cuboid: By specifying the resolutions Nx, Ny and Nz. (Bins denote the granularity at which the volume can be bifurcated into its component media.)

- Positions of each media within the concerned cuboid: By assigning the media index for each voxel in the “GeomFunc” at the end of the model file. The media index is corresponding to the “j” defined in “mediaPropertiesFunc” at the end of the model file. Media definition in “mediaPropertiesFunc” is introduced in Section 3.2 Media Property Model.

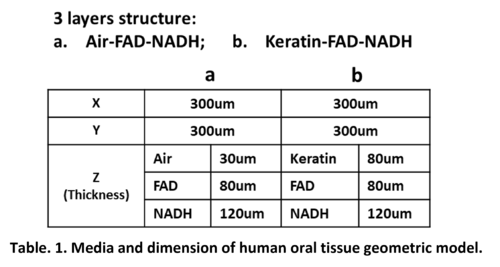
In our study, as introduced in Section 2, human oral tissue can be simplified into a 3-layer structure geometry model: Epithelium layer with FAD and NADH beneath; then with/without Keratin layer on top of it. Therefore, 2 configurations: Air-FAD-NADH and Keratin-FAD-NADH are simulated in our study. For the dimension size of the simulation volume, X and Y are set to 300μm. For the thickness of every single layer Z, we all use the site-specific clinical values in practice, which are obtained from Ref. []. In prior work, Monte Carlo simulation result is found to be very sensitive to the thickness settings. Therefore, using the practical site-specific tissue thickness rather than the general tissue thickness will make our simulation more accurate. In all, please refer to below table for all the geometric parameters used in our MCMatlab simulation.

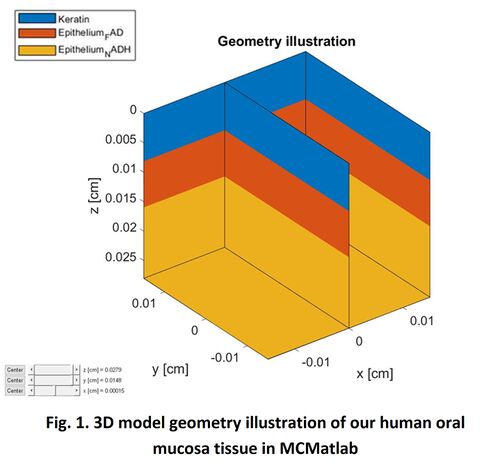
Figure 1 present the 3D model geometry illustration of our human oral mucosa tissue constructed in MCMatlab. The top blue layer is either Air or Keratin; the middle orange layer represents the FAD in epithelium layer; and the bottom yellow layer represents the NADH in epithelium layer.

Media Property Model

Once the geometry set up done, media for each voxel needs to be defined in the next step to complete building up the comprehensive model. In MCMatlab, this can be done by modifying or adding to “mediaPropertiesFunc” at the end of the model file. It may optionally include the fluorescence properties as well. To be more specific, each medium can be specified with three optical parameters and one fluorescent property below:

1. μa — Absorption Coefficient in units of 1/cm. May be (a) scalar, (b) a function handle taking wavelength as input or (c) a function handle taking wavelength, FR, T and FD as inputs.
2. μs — Scattering Coefficient in units of 1/cm. May be (a) scalar, (b) a function handle taking wavelength as input or (c) a function handle taking wavelength, FR, T and FD as inputs.
3. g — The scattering anisotropy (the mean cosine to the scattering angle), to be used in the Henyey-Greenstein phase function. It has no units. May be (a) scalar, (b) a function handle taking wavelength as input or (c) a function handle taking wavelength, FR, T and FD as inputs.
4. QY — The quantum yield of fluorescence, that is, photons of fluorescence emitted relative to excitation photons absorbed. It has no units. May be (a) scalar, (b) a function handle taking wavelength as input or (c) a function handle taking wavelength, FR, T and FD as inputs.

In addition, we need to complete two wavelengths setting as well:

1. Set MonteCarlo wavelength to Excitation wavelength;
2. Set Fluorescence MonteCarlo wavelength to Emission wavelength.

In our study, right after 3-layers geometry built up in Section 3.1, we input all optical parameters of these 4 voxels to “mediaPropertiesFunc” for our simulation:

1. Air Layer

   μa [cm-1]: μa=1e-8 [];
   μs [cm-1]: μs=1e-8 [];
   g: g=1 [];

μa, μs and g for Air are all constants, and the values are obtained from MCMatlab standard tissue example.

1. FAD/NADH/Keratin Layer Layer

   μa [cm-1]:
   a.	μa=3 (non-fluorescent) [];
   b.	μa=A/thickness (fluorescent);

The absorption coefficient is considered different for two conditions. When input light wavelength is beyond excitation range, the fluorophore is not excited and not emit fluorescence, μa is considered as constant 3 for simplification. This assumption and value were used in Ref. []. Otherwise, we use the formula μa=A/thickness for calculation. A is the absorbance, and we use the excitation matrix from each fluorophore EEM for it in our simulation. Apparently, it is wavelength dependent, and should be more accurate than the constant assumption.

   μs [cm-1]:
   μs_FAD/NADH = 51.9*((523/λ_Excitation)^0.6;
   μs_Keratin = 160.3*((523/λ_Excitation)^0.6;

We use the wavelength dependent scattering coefficient empirical formula μs=μ0*((523/λ)^0.6 [] to calculate out μs. This formula is from last year's class report and code. Then we use μs = 66 cm-1 at 350nm (λ) in Ref. [] to calculate out μ0 = 51.9 cm-1 at 523nm for FAD/NADH, and μs = 204 cm-1 at 350nm (λ) for Keratin in Ref. [] to calculate out μ0 = 160.3 cm-1 at 523nm for Keratin. Then substitute μ0_FAD/NADH and μ0_Keratin back to the empirical formula, so that we obtained μs_FAD/NADH and μs_Keratin expression as above. In some paper, people also assume μs is a constant []. But wavelength dependent scattering coefficient empirical is more accurate.

   g: 
   g=0.9 [].

This value is also obtained from MCMatlab "FluorescenceAndImage" example.

   QY:
   QY= EEM/(1-10^(-A))/2;

We use the fluorescence intensity formula

   If=kI0φ[1-(10-εbc)] 

to calculate out the quantum yield of the fluorophore, where If is the fluorescence intensity, I0 is the incident light intensity, k is a proportionality constant attributed to the instrument, ε is the molar absorptivity, b is the path length, and c is the concentration of the substrate. If/I0 is EEM for each fluorophore. φ is the quantum yield; and εbc=A, A is absorbance. We use excitation matrix from each fluorophore EEM to represent A. λ_Excitation, λ_Emission, A, EEM are all extracted from dataset of FAD/NADH/Keratin Excitation Emission Matrixes shared by Prof. Farrell.

μ$_{a}$

Results

We investigated the relation of the tissue fluorescence with respect to different excitation wavelengths. Apparently, the excitation wavelength determined which fluorophore at different tissue depth was excited, and accordingly the final fluorescent emission spectrum and intensity.

Below shows a typical example where FAD, NADH and Keratin layer is excited and fluorescent respectively at the specific excitation wavelength and emission wavelength. For NonKeratin-FAD-NADH 3 layer structure, when the excitation wavelength is 450nm, Fig.XX.(d) shows light is mainly absorbed by FAD layer. FAD is excited and provides the fluorescent emission, as shown in Fig.XX.(j); while when the excitation wavelength is 340nm, Fig.XX.(e) shows light is mainly absorbed by NADH layer. Then NADH is excited and provides the fluorescent emission, as shown in Fig.XX.(k). For Keratin-FAD-NADH 3 layer structure, when the excitation wavelength is 285nm, Fig.XX.(f) shows light is mainly absorbed by Keratin layer. Therefore Keratin is excited and provides the fluorescent emission, as shown in Fig.XX.(l).

Appendix

You can write math equations as follows: $y=x+5$

You can include images as follows (you will need to upload the image first using the toolbox on the left bar, using the "Upload file" link).