Matt

VARIATION IN SIGNIFICANT CLUSTER NUMBER AND DISTRIBUTION DUE TO PARAMETER SELECTION DURING CORRECTION FOR MULTIPLE COMPARISONS USING THE MONTE CARLO METHOD IN FUNCTIONAL MAGNETIC RESONANCE IMAGING DATA

Background

When conducting statistical analysis it is important to be aware of the problem of multiple comparisons. The problem of multiple comparisons arises when more than one statistical test is considered simultaneously. When more than one statistical test is conducted, there is an increased likelihood that any single test will reach significance for rejection of the null hypothesis compared to if a single test were ran. Importantly, criterion for null hypothesis rejection can be altered to help accommodate for multiple statistical tests. One example of multiple comparison correction is the Bonferroni method, which requires the single-test p-value rejection threshold to be divided by the number of tests conducted. For datasets in which many statistical tests are necessary to make inferences, methods like the Bonferroni correction may be too severe, resulting in strongly reduce power.

The problem of multiple comparisons often occurs in statistical analysis of brain imaging data, where analysis can often be conducted on data from more than one channel, voxel, dipole source, temporal bin or spatial location. For example, in functional magnetic resonance imaging (fMRI), there are often more than 10,000 voxels from which data is statistically analyzed. If 10,000 signals were created using a random number generator, simply by chance alone many signals would likely appear to be significant, that is, if not corrected for multiple comparisons. Many methods have been developed to deem whether a particular fMRI signal is significant. One such method uses Monte Carlo simulations.

The Monte Carlo method includes four major steps, first a domain needs to be designated (a space for values), second values need to be assigned to the spaces identified in the first step in a random manner, third and lastly, a pre-specified calculation needs to be ran on these values to assess probability of outcomes. The values should be truly random and many. In fMRI applications, Monte Carlo simulations can be used to assess statistical power of a cluster of voxels identified at a given voxel-wise p-threshold. Such a Monte Carlo simulation may use a volume of voxels as the domain, a random number generator for input assignment (n(0,1) per voxel), and a calculation of the size of clusters at given threshold to quantify probabilities of observed outcomes. Such a Monte Carlo simulation can be repeated multiple times to achieve increasingly precise and stabile estimates, and the resulting cluster sizes can be averaged across iterations.

In the current study, I used a previously collected dataset (detailed below) to explore the effects of parameter selection (voxel-wise p-threshold) in Monte Carlo simulation on the characteristics of significant voxel clusters. The variation in cluster size and distribution is subsequently discussed. I hypothesize that at more stringent voxel-wise p-thresholds the clusters will be smaller and more statistically significant on average, per voxel.

Below is another example of a reinotopic map in a different subject.
Figure 2

Once you upload the images, they look like this. Note that you can control many features of the images, like whether to show a thumbnail, and the display resolution.

Figure 3

Methods

Overview of dataset

Subjects

Nine adults diagnosed with major depressive disorder (MDD). Exclusion criteria included: history of brain injury, primary psychotic ideation, panic disorder, mania, social phobia, post-traumatic stress disorder, substance abuse in past six months, generalized anxiety disorder, left-handedness, hypertension, neurological illness, metal implants, skull fracture history, head trauma with loss of consciousness greater than 5 minutes. Six of the nine subjects were on antidepressants. Depressive symptom severity was assessed using the Beck Depression Inventory (BDI-II; Beck et al. 1979) at the time of scanning and on average 18.7 months later. BDI change scores (time 2 – time 1) were used in voxel-wise correlation analysis with neural activations (described below).

Task

During fMRI scanning, subjects viewed images from the International Affective Picture System (IAPS; Lang & Greenwald 1993) rated negative, neutral, and positive. Images were presented for 2 seconds, after which subjects were to rate the image and fixate. One trial was 14 seconds long (12 seconds rating/fixating). 210 images were viewed, 70 each for negative, neutral and positive. These images were presented in a random order for each subject across five 588-second runs.

One week after MRI data collection, subjects completed an incidental recognition memory task. The task required viewing and rating of 420 IAPS images, 210 of which had been seen during scanning (210 which had not, i.e. foils). Subjects indicated if the image had been previously unseen, was merely familiar or remembered.

MR acquisition

A 1.5T General Electric Signa MR scanner was used to collect functional whole brain data. Scout scans were used to localize brain, with two high-order shims applied thereafter. A single-channel whole head coil was used to acquire blood-oxygen level-dependent (BOLD) data with a spiral pulse sequence (Glover and Law 2001) [24 axial slices, repetition time (TR) = 83 ms/slice, echo time (TE) 40 ms, flip angle = 70°, field of view (FOV) = 24 cm, acquisition time = 2000 ms per frame, number of frames = 299 per run]. Slices had 3.75mm2 in-plane and 4mm through-plane resolution (1mm between-slice distance). A structural scan was then collected for co-registration of the functional data (115 slices, 1 mm2 in-plane and 1.5 mm through-plane resolution, TE = min, flip angle = 15°, FOV = 22cm). A bite-bar formed for each subject was used for head-movement minimization.

MR analysis

Analysis was conducted using the Analysis of Functional NeuroImages (AFNI; afni.nimh.nih.gov) software suite.

Pre-processing and fMRI analysis

Using a Fourier interpolation algorithm BOLD functional images were motion corrected. A despiking algorithm was used to further correct images with 1-3mm movements by replacing data from individual high motion acquisitions with outlier insensitive images. Functional data was then spatially smooth using a full width at half maximum of 4mm Gaussian kernel. Data was high-pass filtered with frequency criterion of one cycle per minute, and subsequently converted to percent signal change. Data were then warped to the Talairach template volume (Talairach & Tournoux 1988).

Response differences for subsequently remembered negative versus subsequently remembered neutral images were calculated as follows. Delta functions were separately created for each subject using ratings from the recognition task. Stimuli events that were rated as being remembered were convolved with a gamma function for creating valence and memory covariates for fitting the signal timecourses at each voxel. AFNI’s 3dDeconvolve was used for least-squares data-fitting on these covariates (after accounting for nuisance covariates). Contrast coefficients from negative versus neutral conditions were obtained using 3dDeconvolve for each participant, resulting in voxel-wise estimates of responses to negative compared to neutral remembered stimuli.

Relating depressive symptomatology to BOLD response

After a pRF model was solved for each subject, the model was trasnformed into MNI template space. This was done by first aligning the high resolution t1-weighted anatomical scan from each subject to an MNI template. Since the pRF model was coregistered to the t1-anatomical scan, the same alignment matrix could then be applied to the pRF model.
Once each pRF model was aligned to MNI space, 4 model parameters - x, y, sigma, and r^2 - were averaged across each of the 6 subjects in each voxel.

Statistical methods

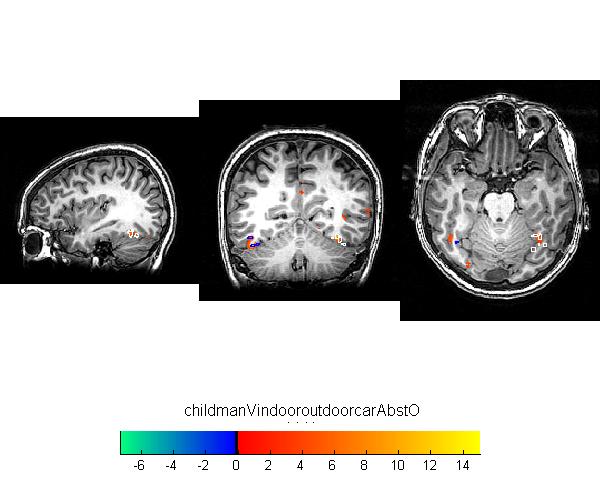
Monte Carlo simulations were conducted using AFNI’s AlphaSim (See Fig. 1 for a schematic of the steps of AlphaSim).

Step 1: AlphaSim fills a nx-by-ny-by-nz image with independent random numbers between 0 and 1. The dimensions of this image are determined by the native space of the fMRI data being assessed (in the current study 54x64x50).

Step 2: A Gaussian filter then applied to the spatially uncorrelated map to simulate voxel correlation. More specifically, AlphaSim accomplishes this filtering by taking the 3D fast Fourier transform (FFT) of the random image, multiplying this by the transform of the Gaussian function, and finally applying inverse FFT to the result. This works because convolution in the space domain is computationally identical to multiplication in the frequency domain. The filter’s parameters should be set to match those used in preprocessing of the test fMRI data, in the current study 4mm FWHM.

Step 3: The resulting image is scaled and thresholded based on the p-threshold parameter values, resulting in a binary image. Scaling is achieved to identify the voxel-wise probability threshold, pthr. From the samples mean and standard deviation, zthr can be identified, such that pthr x nx x ny x nz of the voxels have intensity larger than zthr. Now all the voxels greater than zthr are set to ‘1’, and all voxels less than zthr are set to ‘0’, resulting in a binary image.

Step 4: The binary image of the entire voxel space is then masked with the region of interest. In the current study, a whole brain mask was used. Smaller anatomically or functionally defined volumes can also be used. In theory, reducing the number of voxels from which clusters can be identified from should reduce the cluster size required to reach significance. Step 5: Clusters are then identified from the masked binary image. Clusters are composed of non-zero voxels with adjacent faces. At a given voxel-wise p-threshold, each (activated or non-zero) voxel can only be a member of 1 cluster. All clusters are then identified and recorded in a frequency table.

Steps 1 through 5 are then repeated and the frequency table is updated. Repeating the process allows for increased precision and stability of cluster size estimates. To assess significance, alpha values are then calculated by identifying what percentage of the images have clusters of a given size. The current study explored cluster sizes, frequency and location at voxel-wise p-thresholds of 0.10, 0.05, 0.04, 0.03, 0.02, 0.01, 0.005, and 0.001. 10000 Monte Carlo simulations were initiated.

Results - What you found

Retinotopic models in native space

Some text. Some analysis. Some figures.

Retinotopic models in individual subjects transformed into MNI space

Some text. Some analysis. Some figures.

Retinotopic models in group-averaged data on the MNI template brain

Some text. Some analysis. Some figures. Maybe some equations.

Equations

If you want to use equations, you can use the same formats that are use on wikipedia.
See wikimedia help on formulas for help.
This example of equation use is copied and pasted from wikipedia's article on the DFT.

The sequence of N complex numbers x₀, ..., x_N−1 is transformed into the sequence of N complex numbers X₀, ..., X_N−1 by the DFT according to the formula:

$X_{k}=\sum _{n=0}^{N-1}x_{n}e^{-{\frac {2\pi i}{N}}kn}\quad \quad k=0,\dots ,N-1$

where i is the imaginary unit and $e^{\frac {2\pi i}{N}}$ is a primitive N'th root of unity. (This expression can also be written in terms of a DFT matrix; when scaled appropriately it becomes a unitary matrix and the X_k can thus be viewed as coefficients of x in an orthonormal basis.)

The transform is sometimes denoted by the symbol ${\mathcal {F}}$, as in $\mathbf {X} ={\mathcal {F}}\left\{\mathbf {x} \right\}$ or ${\mathcal {F}}\left(\mathbf {x} \right)$ or ${\mathcal {F}}\mathbf {x}$.

The inverse discrete Fourier transform (IDFT) is given by

$x_{n}={\frac {1}{N}}\sum _{k=0}^{N-1}X_{k}e^{{\frac {2\pi i}{N}}kn}\quad \quad n=0,\dots ,N-1.$

Retinotopic models in group-averaged data projected back into native space

Some text. Some analysis. Some figures.

Conclusions

Here is where you say what your results mean.

References - Resources and related work

References

Software