Murthy

Introduction

The study of human eye movements and vision is an active research field. Over the past 35 years, researchers have focused on a few particular topics of interest, namely smooth pursuit, saccades, and the interactions of these movements with vision. The fundamental question of “how does the motion of the image on the retina affect vision?” has been a continuous area of focus.[1]

The knowledge of how eye movements impact vision has a wide variety of beneficial implications, from augmenting understanding of human behavior to assisting in the development of therapeutics. Eye movement studies have been used since the mid nineteenth century to understand human disease [2], and applications of eye movement research have the potential to alleviate vision disorders (such as the Stanford Artificial Retina Project, which can utilize such research to inform the prosthesis design).[3]

The study of eye movements and their impact on visual acuity can be challenging to conduct in vivo. Noise can be introduced from uncontrollable oculomotor muscle contractions, and it is challenging with human participants to perform repeatable eye movements and obtain an objective measure of their effect on vision. The ISETBio toolbox provides comprehensive functionality to enable the study of human visual acuity in a controlled simulation environment.[4]

The purpose of this project is to modify the eye movement patterns and cone properties of an ISETBio visual model, and observe trends related to the effects of these parameters on the visual acuity of the model. For this project, the Modulation Transfer Function (MTF) is used as an evaluation of visual acuity. The MTF is a curve depicting contrast reduction vs. spatial frequency, and it is a widely accepted research and industry standard method of comparing the performance of two visual systems.[5]

Methods

MTF Computational Pipeline

ISO12233 provides a method for computing the MTF in a fast, standard manner. The MTF is, by definition, the magnitude of the Fourier Transform of the Linespread Function of the optical system. In turn, the Linespread Function is the derivative of the system’s response to an edge.[NUMBER] Using ISETBio and its ISO12233 function, the MTF can be generated by presenting a slanted edge to the visual model, then performing the aforementioned calculations to get from the edge response to the MTF curve.

In this regard, all MTFs for this project were generated via the computational pipeline depicted in Figure NUMBER. First, the “slanted edge” scene is generated. A macular pigment is applied to obtain the optical image of the scene. Second, a cone mosaic is created to produce the retina model. This process is described in more detail below. Third, the eye movement sequence is generated. This process is also described in more detail below. Fourth, the optical image is presented to the cone mosaic. The photon absorptions of each cone in the mosaic are computed for each time step (in this case, 5 milliseconds). Every time step, the presented image is shifted in accordance with the single eye movement for that time step. Finally, the mean absorptions for the cone mosaic are used to generate the MTF via the ISO12233 function. This process is repeated for the desired number of trials, producing one MTF per trial.

Figure NUMBER: MTF Generation Process

Generating Cone Mosaics

In order to execute the process depicted above, it was first necessary to generate the cone mosaics that would be used. For this project, it was desired to model two portions of the retina- the center of the fovea, and slightly to the periphery. For each model, a rectangular cone mosaic was generated using the “coneMosaic” method in ISETBio.

First the “center” model was created. This cone mosaic is meant to represent the photoreceptors at the center of the fovea. Using the knowledge from Foundations of Vision that the S cones are absent at the center of the fovea [6], this model was created by specifying an even distribution of L and M cones, with no S cones and no blank spaces. The “coneMosaic” method in ISETBio defaults to generating cones with an aperture that is representative of the center of the fovea, so no special parameters needed to be set with respect to aperture. In this model, the aperture size was 1.4 micron. The “center” cone mosaic is depicted in Figure NUMBER below.

Second, the “periphery” model was created. This cone mosaic is intended to represent the photoreceptors at a few degrees eccentricity relative to the center of the fovea. Initially, I considered making a mosaic that included blank spaces, which would represent rods. However, when attempting to run the ISO12233 routine using a model with blank cones, the resultant MTFs appeared to have erroneous shapes, indicating computational difficulty.

To address this issue while still attempting to generate a relatively accurate retinal model, the periphery model was chosen to represent 2 degrees of eccentricity. This decision was based on Figure 3.1 from Foundations of Vision (linked) [6], which depicts the density of rods and cones as one moves across the retina. It is clear to see that while cone density falls off rapidly as one moves peripherally from the fovea, there is still a high concentration of cones at 2 degrees of eccentricity. To determine the aperture size for these cones, the ISETBio function “coneSizeReadData” was used. This function uses data from Curcio et. al. Figure 6, below, to estimate cone aperture size from cone density data.[NUMBER] Using this method, the cone aperture size for the periphery model was 3.89 micron. This mosaic is also depicted in Figure NUMBER below.

Generating Eye Movement Sequences

For this project, it was desired to create a wide variety of relatively realistic eye movements. In addition to specifying a blank set of eye movements to provide a stationary baseline for later comparison, three distinct eye movement types were modelled: fixational, nystagmus, and drift. All sequences were coded into the model by setting the “coneMosaic.emPositions”.

First, the fixational eye movements were generated. These were made by using the ISETBio built-in functionality, which defaults to the creation of random, small amplitude microsaccades.

Second, the nystagmus eye movements were added. These sequences could not be generated using a built-in ISETBio function, so they were custom programmed. Nystagmus is characterized by rapid, oscillatory eye movements, so these sequences consist of rapid flicks of the eyes back and forth. With these movements, it was desirable to investigate the effects of orientation and amplitude on the resultant visual acuity. Therefore, four separate Nystagmus sequences were created – horizontal, vertical, parallel, and perpendicular.

For the horizontal and vertical sequences, one specifies an amplitude in number of cones on the cone mosaic. The eye positions flick between the positive and negative values of that amplitude with each time step. To attempt to make the movements slightly more realistic, a “jitter” parameter was also added that created a small amount of perpendicular movement. For example, one horizontal sequence could have an amplitude of 8 cones to the left and right, but then “jitter” up and down by 1 or 2 cones. This is meant to model oculomotor contractions, which will not necessarily be perfectly along one axis.

For the parallel and perpendicular sequences, the amplitude is fixed to be ~5 cones. The parallel path is designed such that its slope matches the slope of the slanted edge that is being presented to the visual model, and the perpendicular path is perpendicular to the slanted edge scene.

The fixational and nystagmus movement sequences are depicted in Figure NUMBER below.

Finally, the drift sequence was added. For this sequence, it is only horizontal, and there is not jitter involved. One can specify an amplitude in cones of the mosaic, and the eye will drift to the positive and negative of that amplitude, but will only do this once over the entire course of the movement sequence. This is a much slower movement in relation to the nystagmus movements. The difference between the drift and nystagmus sequence can be seen in Figure NUMBER below.

Automated Script

To allow investigation of the effects of these input parameters on the output MTF, a MATLAB script was developed to automate the MTF generation process. This script is attached in Appendix I, and can be used by current and future students to both validate the results presented here and to continue similar investigations in future projects. The script allows a user to specify which model type they’d like to use (and define degrees of eccentricity for the periphery model), select one type of eye movement pattern (and set defining characteristics such as amplitude), specify the number of eye movements and number of trials, and specify whether photon noise is present. Once those parameters have been defined, the script will run the desired number of trials, store all MTF info from the ISO12233 routine, and plot all the MTFs in one figure. It will also keep track of some characteristic statistics, as will be discussed further in the Results section.

Results

Noise

Upon beginning to modify parameters and generate MTFs, it quickly became clear that the MTF curves being generated were not consistent from one run to the next. Three sources of noise were identified as contributing factors. (1) The cone mosaic pattern was randomly generated. Although the ratio of cone types was consistent, their particular locations were not. (2) Photon noise was present in the model. This is a physically accurate representation that is built into the ISETBio cone absorptions. (3) Certain eye movement patterns had variability. Fixational eye movements were randomized, and the “jitter” components of nystagmus were random.

To attempt to eliminate this noise and look first at the cleanest possible trends between input parameters and effect on MTF, a third cone mosaic model was generated, referred to as “control”. This mosaic consists entirely of “L” cones, has the same standard foveal cone aperture of 1.4 micron, and has photon noise disabled.

Not all of the noise could be eliminated from the control model, as some eye movements still had randomness. Furthermore, it would be necessary to add noise back in when assessing the center and periphery models. To account for this variation in MTF curves, the MTF50 metric was identified as a proxy for visual acuity. This metric represents where contrast reaches half of its peak, and it is a standard way of comparing optical systems. Since the MTF50 was relatively consistent across many trials with variable MTFs, the mean MTF provides a good indication of the visual acuity of the system.

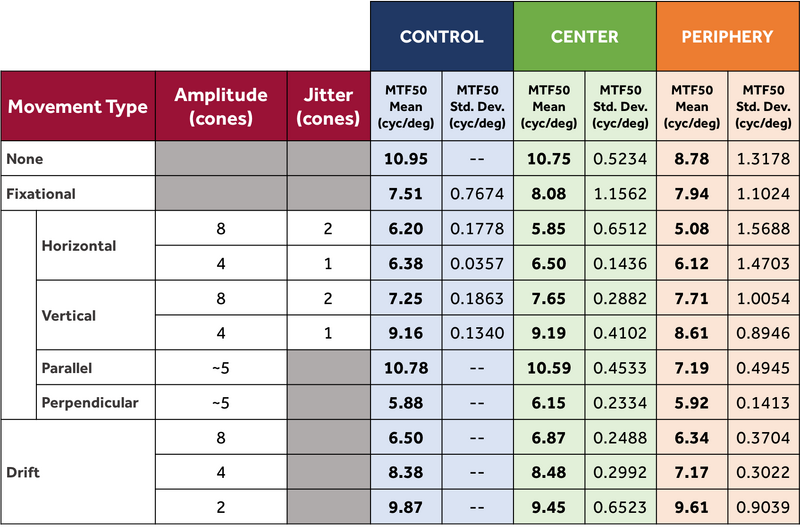
Final Results Table

For each eye model and movement sequence in the table below, 50 eye movements were used, and 100 trials were conducted.

Conclusions

Key Findings

To summarize:

Fixational eye movements were found to reduce visual acuity, which is in line with part of the fatigue theory. However, the full fatigue theory could not be validated because fatigue is not currently built into the cone absorptions in ISETBio.

The orientation of nystagmus movements was found to be highly correlated with visual acuity. The closer the movements are to matching the slanted edge orientation, the smaller the distortion of the scene over the mean cone absorptions, and the higher the visual acuity. Lower amplitude eye movements were associated with higher visual acuity. Slower eye movements were associated with higher visual acuity.

These trends all mostly held for both the center and periphery models. On aggregate, the periphery model was found to have diminished visual acuity as compared to the center model. It also had much higher MTF50 standard deviations, due to computational challenges with the ISO12233 routine.