Psych221 Pipeline

Processing Pipeline Project for Psych 221

Currently this page is not linked anywhere while it is being worked on.

We provide noisy sensor images and desired sRGB renderings of those images. Your implement processing algorithms (color transform(s), denoising, demosaicking, and display rendering steps) to approximate the high quality desired sRGB renderings. This can (and should) be a team project with students who implement different parts of the image processing pipeline. We evaluate your methods by providing new test images for your pipeline and evaluate the quality of the sRGB rendering.

The goal of this project is to implement and evaluate an image processing pipeline to take raw output from a camera sensor and generate a pleasing image of the original scene.

The project involves two important steps:

• Leverage existing image processing algorithm(s) to generate a functioning pipeline.
• Evaluate the perceptual quality of the rendered images.

Processing Pipeline Background

A number of calculations are required to take the output from a camera sensor and generate a nice sRGB image.

• Demosaicking: In almost all sensors for color imaging, individual photoreceptors (pixels) have one of a few optical filters placed on them so the photoreceptor measures only a particular color of light. These optical filters over each individual pixel make up the color filter array (CFA). Demosaicking is the process of estimating the unmeasured color bands at each pixel to generate a full color image.
• Denoising: Since measurements from the sensor contain noise, denoising attempts to remove any unwanted noise in the image while still preserving the underlying content of the image.
• Color transformation: A color transformation is necessary to convert from the color space measured by the sensor into a desired standard color space such as XYZ or sRGB.

There are more steps in real pipelines but these are the most challenging and the relevant ones for this project. There are dozens of algorithms published for both demosaicking and denoising. Traditionally pipelines contain these calculations as independent steps.

Recently some researchers have suggested combining the demosaicking and denoising calculations into a single algorithm that performs both calculations. Although a combined approach is not required for the project, we recommend it. Implementing and understanding a single algorithm is much easier than implementing two totally separate algorithms.

The easiest color transform you could implement is a linear transformation (multiply by 3x3 matrix) from the sensor's color space to XYZ. But there are reasons this may be improved especially for low noise. Maybe your project will improve upon this basic approach, maybe not.

Selected Existing Algorithms

The following are algorithms that perform demosaicking and denoising. The authors have provided a Matlab implementation, although I cannot vouch for the quality of the code. Feel free to pick an algorithm from this list, use one you find from the literature, or create your own approach. If you intend to use a particular algorithm, please let me know so other students do not pick the same one.

• D. Paliy, A. Foi, R. Bilcu and V. Katkovnik, "Denoising and interpolation of noisy Bayer data with adaptive cross-color filters," in 2008, pp. 68221K. [1]

• K.Hirakawa, T.W. Parks, "Joint Demosaicing and Denoising." [2] (and related papers from site)

• L. Zhang, X. Wu, and D. Zhang, "Color Reproduction from Noisy CFA Data of Single Sensor Digital Cameras," IEEE Trans. Image Processing, vol. 16, no. 9, pp. 2184-2197, Sept. 2007. [3]

• L. Condat, “A simple, fast and efficient approach to denoisaicking: Joint demosaicking and denoising,” IEEE ICIP, 2010, Hong Kong, China. [4]

The noise model assumed by these algorithms may be different than the one built into ISET. For instance, many authors of denoising papers assume additive white Gaussian noise, which is not as realistic as ISET's noise model. Often denoising algorithms require some parameter to describe the noise level in the image. One challenge in this project is finding the right noise parameter value for your algorithm. If you overestimate the noise level, the algorithm may oversmooth the image and lose important image features. If you underestimate the noise level, the algorithm may not sufficiently filter out the noise. Rely on the S-CIELAB metric to make decisions about how to choose such a parameter to give the most pleasing result.

Software

Image Data

We are providing 6 images to design and test your pipeline. They are 'imageset_#.mat' in the 'Data' folder. Each file contains a number of variables. The most important are:

• cfa: The ideal noise-free image obtained by a camera's sensor for a particular light level. The color filter array (CFA) on the sensor is the Bayer pattern shown below. The top-left pixel represents a red measurements, etc. To simulate the output from an actual sensor, this image is adjusted to the correct light level and then the noise process is simulated.

• imXYZ: The ideal image you would like to come out of your pipeline. The image contains 3 channels corresponding to the XYZ color matching functions at each pixel. For instance, imXYZ(:,:,1) is the X measurement at each pixel. These were calculated from a multispectral description of the scene so is considered to be the goal of the pipeline. Although you won't be able to exactly create these images from the noisy CFA measurements, your goal is for images from your pipeline to be as perceptually similar as possible.

• inputfilters: The camera's sensitivity for the R, G, and B channels, which are shown below. This determines the color properties of the sensor. Specifically the sensitivity is the probability that an incident photon of a particular wavelength excites an electron-hole pair that is detected by the sensor, so [R;G;B]=inputfilters'*light. The relative sensitivities are from a Nikon D100 camera.

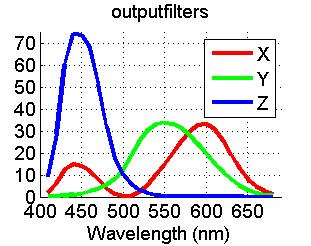
• outputfilters: The XYZ filters that were used to generate imXYZ, which are shown below. They are adjusted slightly from the standard XYZ functions so the XYZ calculation is identical to the camera calculation, [X;Y;Z]=outputfilters'*light.

• wave: Vector giving the samples of the wavelength in nm. This is always 410:10:680.

Evaluation

Since there are lots of algorithms that one could use for a image processing pipeline, it is important to know how well the pipelines work. To do this we need to have a method for evaluating the perceptual quality of the output images. Each image file in the software package includes a variable "imXYZ" that is the ideal XYZ image for the scene. The images from the pipelines of course can never be exactly the same as these ideal images due to sampling and noise. We will primarily use Spatial CIELAB (S-CIELAB) to quantify the perceptual significance of the the differences between the images.

In your project, please present or address the following issues:

• Show some example images for the different light levels. (The script showresultimages.m should be helpful.)
• Under what conditions are the differences between images from your pipeline and the ideal images visible? (By conditions I mean light levels, images, or image features.)
• Under what conditions are the differences between images from your pipeline and the simple pipeline visible or significant?
• Are there any images or image features that are particularly easy or challenging for your pipeline.
• How accurate are the colors produced by your pipeline? Does this change for different light levels? Show the MacBeth Color Checker for the different light levels.
• How well does the pipeline eliminate noise in smooth regions of the image? (Use MacBeth Color Checker.)

Assistance

Send questions to Steven Lansel, slansel@stanford.edu.