Psych221 Pipeline
This describes the processing pipeline project offered for Psych 221 in Winter, 2011.
We provide (noisy) sensor images and desired renderings of those images. You implement the processing algorithms (color transform(s), denoising, demosaicking, and display rendering steps) to achieve the high quality desired renderings. We evaluate your methods by providing new test images for your pipeline and evaluate the quality of the sRGB rendering.
The goal of this project is to implement and evaluate an image processing pipeline that converts output from a camera sensor (volts at each pixel) into a pleasing (and accurate) image of the original scene.
The project involves two important steps:
- Leverage existing image processing algorithm(s) to generate a functioning pipeline.
- Evaluate the perceptual quality of the rendered images.
This can (and should) be a team project; different students will implement different parts of the image processing pipeline.
Background
A number of calculations are required to take the output from a camera sensor and generate a nice sRGB image.
- Demosaicking: In almost all sensors for color imaging, individual photoreceptors (pixels) have one of a few optical filters placed on them so the photoreceptor measures only a particular color of light. These optical filters over each individual pixel make up the color filter array (CFA). Demosaicking is the process of estimating the unmeasured color bands at each pixel to generate a full color image.
- Denoising: Since measurements from the sensor contain noise, denoising attempts to remove any unwanted noise in the image while still preserving the underlying content of the image.
- Color transformation: A color transformation is necessary to convert from the color space measured by the sensor into a desired standard color space such as XYZ or sRGB.
There are more steps in real pipelines but these are the most challenging and the relevant ones for this project. There are dozens of algorithms published for both demosaicking and denoising. Traditionally pipelines contain these calculations as independent steps.
Recently some researchers have suggested combining the demosaicking and denoising calculations into a single algorithm that performs both calculations. Although a combined approach is not required for the project, we recommend it. Implementing and understanding a single algorithm is much easier than implementing two totally separate algorithms.
The easiest color transform you could implement is a linear transformation (multiply by 3x3 matrix) from the sensor's color space to XYZ. But there are reasons this may be improved especially for low noise. Maybe your project will improve upon this basic approach, maybe not.
Selected Existing Algorithms
The following are algorithms that perform demosaicking and denoising. The authors have provided a Matlab implementation, although I cannot vouch for the quality of the code. Feel free to pick an algorithm from this list, use one you find from the literature, or create your own approach. If you intend to use a particular algorithm, please let me know so other students do not pick the same one.
- ***Taken by a group*** D. Paliy, A. Foi, R. Bilcu and V. Katkovnik, "Denoising and interpolation of noisy Bayer data with adaptive cross-color filters," in 2008, pp. 68221K. [1]
- K.Hirakawa, T.W. Parks, "Joint Demosaicing and Denoising." [2] (and related papers from site)
- ***Taken by a group*** L. Zhang, X. Wu, and D. Zhang, "Color Reproduction from Noisy CFA Data of Single Sensor Digital Cameras," IEEE Trans. Image Processing, vol. 16, no. 9, pp. 2184-2197, Sept. 2007. [3]
- ***Taken by a group*** L. Condat, “A simple, fast and efficient approach to denoisaicking: Joint demosaicking and denoising,” IEEE ICIP, 2010, Hong Kong, China. [4]
The noise model assumed by these algorithms may be different than the one built into ISET. For instance, many authors of denoising papers assume additive white Gaussian noise, which is not as realistic as ISET's noise model. Often denoising algorithms require some parameter to describe the noise level in the image. One challenge in this project is finding the right noise parameter value for your algorithm. If you overestimate the noise level, the algorithm may oversmooth the image and lose important image features. If you underestimate the noise level, the algorithm may not sufficiently filter out the noise. Rely on the S-CIELAB metric to make decisions about how to choose such a parameter to give the most pleasing result.
Provided Software
To assist you in the project, we have setup some data and scripts. The following file contains images and scripts as described below. File:PipelineProject.zip
The images saved in this file were generated by executing the script 'multispectral2images.m' in the following file. This isn't necessarily needed to do the project but is provided for reference and if helpful can be used in any way. File:MakeImageSets.zip
Provided Image Data
We are providing 7 images to design and test your pipeline. Images 1-6 are natural scenes and have filenames 'imageset_#.mat' in the 'Data' folder. The other image, 'imageset_MCC.mat', is a synthetic MacBeth Color Checker. This target has 24 uniform squares with different colors. It is commonly used to test color accuracy and noise in a uniform area.
Each file contains a number of variables. The most important are:
- cfa: The ideal noise-free image obtained by a camera's sensor for a particular light level. The color filter array (CFA) on the sensor is the Bayer pattern shown below. The top-left pixel represents a red measurements, etc. To simulate the output from an actual sensor, this image is adjusted to the correct light level and then the noise process is simulated.
- imXYZ: The ideal image you would like to come out of your pipeline. The image contains 3 channels corresponding to the XYZ color matching functions at each pixel. For instance, imXYZ(:,:,1) is the X measurement at each pixel. These were calculated from a multispectral description of the scene so is considered to be the goal of the pipeline. Although you won't be able to exactly create these images from the noisy CFA measurements, your goal is for images from your pipeline to be as perceptually similar as possible.
- inputfilters: The camera's sensitivity for the R, G, and B channels, which are shown below. This determines the color properties of the sensor. Specifically the sensitivity is the probability that an incident photon of a particular wavelength excites an electron-hole pair that is detected by the sensor, so [R;G;B]=inputfilters'*light. The relative sensitivities are from a Nikon D100 camera.
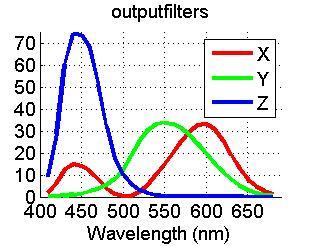
- outputfilters: The XYZ filters that were used to generate imXYZ, which are shown below. They are adjusted slightly from the standard XYZ functions so the XYZ calculation is identical to the camera calculation, [X;Y;Z]=outputfilters'*light.
- wave: Vector giving the samples of the wavelength in nm. This is always 410:10:680.
More Provided Software (Scripts)
- wrapperimage: Sample script that shows how to setup the calculations. It adjust the light level to various mean luminance values, simulates noise, performs a simple pipeline, and calculates SNR and S-CIELAB metrics for the resultant image. Modify the script to run with your pipeline. Output images for each light level and image will be automatically saved and compared with the ideal output to give SNR and S-CIELAB values. The metrics are calculated excluding a border of width 10 pixels around the outside of the image, so the edges are not important for the metric. Once all images are calculated, a file called 'metrictable.mat' is saved that has the SNR and S-CIELAB values for all of the light levels and images in a single place.
- generatenoise: Simulates the noise in a digital camera using the model in ISET. This is for specific camera model parameters that are saved in the data. For simplicity, saturation has been disabled so no measurement is too large for the pixel.
- simplepipeline: Very basic pipeline that performs bilinear demosaicking and linear color correction. This has no denoising so performs very badly at low light levels. You should be able to outperform this pipeline.
- showresultimages: Example script to display output images. Since the images are in XYZ we convert to sRGB for display. Script displays correct image and outputs for all light levels.
- metricplots: Basic script showing some example plots that may be useful.
Evaluation Methods
Since there are lots of algorithms that one could use for an image processing pipeline, it is important to know how well the pipelines work. To do this we need to have a method for evaluating the perceptual quality of the output images. Each image file in the software package includes a variable "imXYZ" that is the ideal XYZ image for the scene. The images from the pipelines of course can never be exactly the same as these ideal images due to sampling and noise. We will primarily use Spatial CIELAB (S-CIELAB) to quantify the perceptual significance of the differences between the images.
In your project, please address the following questions:
- Show some example images for the different light levels. (The script showresultimages.m should be helpful.)
- Under what conditions are the differences between images from your pipeline and the ideal images visible or annoying? (By conditions I mean light levels, images, or image features. The errorImage output from scielabfind should be helpful to look at image features.)
- Under what conditions are the differences between images from your pipeline and the simple pipeline visible or annoying?
- How accurate are the colors produced by your pipeline? Does this change for different light levels? (The MCC Color Bias plot from metricplots.m should be helpful.)
- How well does the pipeline eliminate noise in smooth regions of the image? (The MCC Color Noise plot from metricplots.m should be helpful.)
- What are the computational requirements of the algorithm? Can you break the pipeline down into smaller pieces and show how much computation is required for each piece? (Computation time is a fine description. A relevant plot is made by 'metricplots.m' but will need to be modified for your pipeline.)
Helpful and Friendly Assistance
Send questions to Steven Lansel, slansel@stanford.edu.