Water Surface Mesh Improvements for Underwater Imaging Simulations

Introduction

- Motivate the problem. Describe what has been done in the past.

Background

Underwater imaging is difficult largely due to light attenuation. Attenuation in this case refers to the reduction in the intensity of light as it passes through the water. Water behaves differently than air, so attenuation must be handled differently in underwater imaging.

Fig. 1: Simplification of the different ways that light interacts with water as a medium.

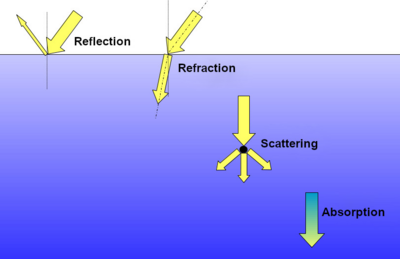
Absorption The absorption of light, in the scope of this project, is caused by the water molecules of the medium interacting with certain energy levels of light, and consequently absorbing specific wavelengths of light. Light absorption directly affects the quantity and energy level of the light that a camera will use at an imaging location.

Scattering Light interacts with water molecules and impurities to be absorbed and re-emitted differently. The resulting light rays have a deviated path, and they may have a different wavelength.

Methods

- Describe techniques you used to measure and analyze. Describe the instruments, and experimental procedures in enough detail so that someone could repeat your analysis. What software did you use? What was the idea of the algorithms and data analysis?

Simulation Tools

For this project, we have used three simulation tools:

• iset3d toolbox We used the iset3d toolbox in MATLAB to provide a physically-accurate ray traced rendering of 3D scenes.

• PBRT We Ran PBRT in MATLAB to produce physically accurate images by physically based and ray tracing through scenes.

• Docker The implementation of iset3d with PBRT is available in a set of Docker containers.

Technique

• include baseline perfect cube/pbrt here

Sine Wave

To more accurately represent natural water surfaces, the first approach was to use a sine wave pattern along the face of the cube that the camera is pointed to captured the scene. The flat, uniform top face of the cube does not adequately simulate the variability characteristic of natural water surfaces. To address this limitation, this method aimed to develop additional geometric modifications that can be implemented to create wave-like patterns on the cube's surface.

The modifications to the cube's geometry, aimed at replicating water surface characteristics, involved the following transformations:

Rectangular Prisms Initially, the cube was transformed into a rectangular prism by extending its length to align with the dimensions of the target face within the scene. Multiple rectangular prisms were then arranged in a repeating pattern across the face of the cube. This arrangement was achieved through a for loop, which determined the number of prisms based on the specified width of the prisms, spacing between them, and the overall width of the target face.

Trapezoidal Prisms To introduce a closer approximation to the curvature of a sine wave, the rectangular prisms were modified into trapezoidal prisms with slanted sides. This intermediate transformation introduced gradual undulations to the cube’s initial flat surface, enhancing its resemblance to natural waveforms. The method for generating and positioning the trapezoidal prisms is similar to that of the rectangular prisms, with the primary difference being the adjustment of the vertices on the top face of the cube.

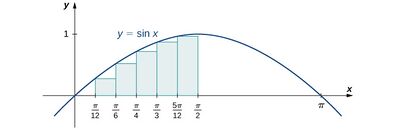
Sine Wave Approximation with Rectangular Prisms Building on the previous methods, a sine wave pattern was approximated using multiple rectangular prisms of varying heights. Five rectangles were used to follow the equation $y=sin(x)$, where x values were set to pi/12, pi/6, pi/4, pi/3, 5pi/12, and pi/2. The heights of the cubes were then scaled in order to create a visible wave pattern. This approach captured the oscillations of a sine wave, resulting in a more realistic simulation of natural water surface dynamics. The rectangular prisms all had the same height and width, with the height of the prism changing depending on location across the cube.

Fig. 2: Representation of sine wave approximation using rectangles.

These transformations were integrated into the scene while preserving the realistic scattering and absorption properties of the original cubic medium. This iterative approach effectively balanced geometric complexity with computational efficiency.

Blue Noise

In some computer graphic applications, designers use blue noise dithering to texture the surface of water in a non-photorealistic way. Blue noise is a sampling pattern that adds an aspect of uniformity to random sampling. In layman's terms, a set of points satisfies blue noise sampling if all points have a random location whilst maintaining an approximately standard distance between each other. Poisson-Disc sampling is one possible method of obtaining this set of points, and it was the method of choice for texturing the cube face in this study.

Modifying the cube face geometry involved the following steps:

Blue Noise Locations Treating the sampling points as pixels, small meshes can be added to the cube face at each pixel location. To execute this, a Poisson-Disc sampling function takes in boundary conditions, minimum point distances, and a specified number of points to generate the desired pixel locations.

Cube Pixels Multiple cube meshes were created and shrunken down to act as “pixels” for the blue noise texture. Each cube-pixel was then added to the cube face in each pixel location. This was done in a loop, where each cube-pixel was individually created and added to the respective pixel location indicated at the time.

Trapezoidal Pixels To observe a surface pattern that is a closer approximation to random destructive wave patterns, the method was repeated with trapezoidal-shaped “pixels” instead. Each trapezoidal-pixel was added to the cube face in a similar method as the cube-pixels, with the core difference being the defined trapezoidal geometries being used for each pixel instead of a cube geometry.

Results

- Organize your results in a good logical order (not necessarily historical order). Include relevant graphs and/or images. Make sure graph axes are labeled. Make sure you draw the reader's attention to the key element of the figure. The key aspect should be the most visible element of the figure or graph. Help the reader by writing a clear figure caption.

Conclusions

- Describe what you learned. What worked? What didn't? Why? What should someone next year try?

References

- List references. Include links to papers that are online.

Appendix I

- Upload source code, test images, etc, and give a description of each link. In some cases, your acquired data may be too large to store practically. In this case, use your judgement (or consult one of us) and only link the most relevant data. Be sure to describe the purpose of your code and to edit the code for clarity. The purpose of placing the code online is to allow others to verify your methods and to learn from your ideas.

Appendix II

- (for groups only) - Work breakdown. Explain how the project work was divided among group members.

Bridget:

Caelia:

Brian: