Water Surface Mesh Improvements for Underwater Imaging Simulations
Introduction
Motivation
Underwater imaging is an important problem in the field of computer graphics due to a variety of factors, including the difficulty of the problem itself and the central role the idea of submerging cameras in a medium is in rendering. In the film industry, we look to movies like Avatar 2, which make extensive use of underwater imaging, while in academia, we have studies looking at the role of underwater imaging in enhancing the quality of images taken from an underwater perspective (Wang et al. 2023). While the rendering of the scene itself has already been done well, one aspect that it lacks is the proper rendering of the surfaces of water. This affects the actual render in two ways. The first, which is in a non-underwater frame of reference, looking at the surface itself. The second, which we are focusing on, is the effect it has on our actual underwater frame of reference in the way it casts shadows onto the underwater scene. By doing this, we hope to be able to generate underwater images that are more realistic.
Previous Work
Our work is based on two categories of previous work. The first is the rendering of the underwater scene itself. We primarily derived this from a modified version of ISET3D's tutorial script, which generates a simple baseline from which we will build up. The second is the modification of the surface of the underwater scene as mentioned above, and we chose several methods based on prior knowledge of water surface movements.
Background
Underwater imaging is difficult largely due to light attenuation. Attenuation in this case refers to the reduction in the intensity of light as it passes through the water. Water behaves differently than air, so attenuation must be handled differently in underwater imaging.
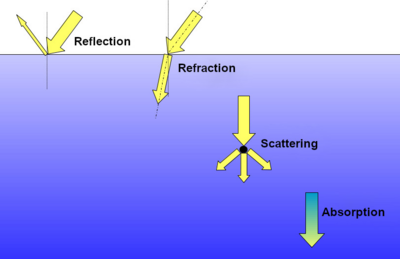
Absorption
The absorption of light, in the scope of this project, is caused by the water molecules of the medium interacting with certain energy levels of light, and consequently absorbing specific wavelengths of light. Light absorption directly affects the quantity and energy level of the light that a camera will use at an imaging location.
Scattering
Light interacts with water molecules and impurities to be absorbed and re-emitted differently. The resulting light rays have a deviated path, and they may have a different wavelength. These parameters are customizable, and for the scope of this project, they were fixed for the best visibility of the rendered image.
Methods
Simulation Tools
For this project, we have used three simulation tools:
- iset3d toolbox We used the iset3d toolbox in MATLAB to provide a physically-accurate ray traced rendering of 3D scenes.
- PBRT We Ran PBRT in MATLAB to produce physically accurate images by physically based and ray tracing through scenes.
- Docker The implementation of iset3d with PBRT is available in a set of Docker containers.
Technique
We begin with the baseline created using a modified version of the ISET3D repository's tutorial code. With it, we use ISET3D to build up a recipe for a scene containing two things. The first is the actual water itself, which has variations depending on the type of water we want to render (seawater or freshwater). The water is created as a simple cube, with 6 flat surfaces. The second is the object within the scene that is used to visualize the actual effects of the medium as well as any other factors, in our case the shadows cast by the surface. For our object, we used a Macbeth Chart. After the recipe is generated, it is passed into PBRT (Physically Based Rendering Tool). PBRT renders the scene using rules derived from the way real optics work by creating simulated lights and materials, and then rendering the way the two interact with each other. The reason this is our baseline is that while the rendering of the medium itself is quite good, it doesn't accurately represent what a real scene would look like; an ocean's surface is never perfectly flat.
Geometric Modifications
This method aimed to develop and explore geometric modifications that can be implemented to create wave-like patterns on the cube's surface. The new pattern was implemented on the face of the cube that points towards the camera.
The modifications to the cube's geometry, aimed at replicating water surface characteristics, explored the following transformations:
Rectangular Prisms Initially, the cube was transformed into a rectangular prism by extending its length to align with the dimensions of the target face within the scene. Multiple rectangular prisms were then arranged in a repeating pattern across the face of the cube. This arrangement was achieved through a for loop, which determined the number of rectangular prisms based on the specified width of the prisms, spacing between them, and the overall width of the target face.
Trapezoidal Prisms To introduce a closer approximation to the curvature of a sine wave, the rectangular prisms were modified into trapezoidal prisms with slanted sides. This intermediate transformation introduced gradual undulations to the cube’s initial flat surface, enhancing its resemblance to natural waveforms. The method for generating and positioning the trapezoidal prisms is similar to that of the rectangular prisms, with the primary difference being the adjustment of the vertices on the top face of the cube.
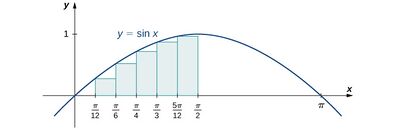
Sine Wave Approximation with Rectangular Prisms Building on the previous methods, a sine wave pattern was approximated using multiple rectangular prisms of varying heights. Five rectangles were used to follow the equation , where x values were set to pi/12, pi/6, pi/4, pi/3, 5pi/12, and pi/2. The heights of the cubes were then scaled in order to create a visible wave pattern. This approach captured the oscillations of a sine wave, resulting in a more realistic simulation of natural water surface dynamics. The rectangular prisms all had the same height and width, with the height of the prism changing depending on the location across the cube.
These transformations were integrated into the scene while preserving the realistic scattering and absorption properties of the original cubic medium. This iterative approach effectively balanced geometric complexity with computational efficiency.
Blue Noise
In some computer graphic applications, designers use blue noise dithering to texture the surface of water in a non-photorealistic way. Blue noise is a sampling pattern that adds an aspect of uniformity to random sampling [BN ref]. In layman's terms, a set of points satisfies blue noise sampling if all points have a random location whilst maintaining an approximately standard distance between each other. Poisson-Disc sampling is one possible method of obtaining this set of points [PD ref], and it was the method of choice for texturing the cube face in this study.
Modifying the cube face geometry involved the following steps:
Blue Noise Locations Treating the sampling points as pixels, small meshes can be added to the cube face at each pixel location. To execute this, a Poisson-Disc sampling function takes in boundary conditions, minimum point distances, and a specified number of points to generate the desired pixel locations.
Cube Pixels Multiple cube meshes were created and shrunken down to act as “pixels” for the blue noise texture. Each cube-pixel was then added to the cube face in each pixel location. This was done in a loop, where each cube-pixel was individually created and added to the respective pixel location indicated at the time.
Trapezoidal Pixels To observe a surface pattern that is a closer approximation to random destructive wave patterns, the method was repeated with trapezoidal-shaped “pixels” instead. Each trapezoidal-pixel was added to the cube face in a similar method as the cube-pixels, with the core difference being the defined trapezoidal geometries being used for each pixel instead of a cube geometry.
Results
Geometric Modifications
The geometric modifications to approximate wave patterns can be evaluated through the following images.
Rectangular Prisms
-
Depiction of rectangular prism pattern
-
Depiction of rectangular prism pattern using more rectangles
Trapezoidal Prisms
-
Depiction of trapezoidal prism pattern
Sine Wave Approximation with Rectangular Prisms
-
Depiction of sine wave pattern without the cube
-
Depiction of the sine pattern waves shape
-
Depiction of original cube with the sine wave pattern added
Blue Noise
The modifications used to approximate blue noise texturing can be seen through the following steps:
Cube Pixels
-
Depiction of cube-pixels in poisson-disc locations, without the cube.
-
Depiction of the cube-pixels applied to the surface of the main water cube.
-
Close-up of submerged Macbeth chart. The blue noise texture with cube-pixels casts faint shadows in random locations.
Trapezoidal Pixels
-
Depiction of trapezoid-pixels in poisson-disc locations, without the cube BEFORE being shrunken to the correct size.
-
Depiction of the trapezoid-pixels applied to the surface of the main water cube.
-
Close-up of submerged Macbeth chart. The blue noise texture with trapezoid-pixels casts faint shadows in random locations.
Conclusions
The images rendered in the prior results section show that both geometric modifications and the addition of blue noise both add realistic texture to the cube. Through both of these methods, we learned that the simplest way to add texture to the scene is to modify the existing cube geometry into rectangular and trapezoidal prisms and add them in a desired pattern.
While we were able to get results using approximation built with cubes and trapezoid, something we hoped to get working was a method that directly used a mesh. We defined a mesh using a set of vertices and combinations of those vertices. This would give us a mesh of triangles, allowing us to create a much more accurate surface. However, we ran into a problem with ISET3D and PBRT, where, even though the points were calculated, it wouldn't render the images properly. The primary method we attempted to implement with this was a 2D sine wave, simulating droplets on a surface. In the future, if this method were to work, it would greatly simplify our rendering process, and allow us to try different, more complex meshes.
References
- Don P. Mitchell. 1991. Spectrally optimal sampling for distribution ray tracing. SIGGRAPH Comput. Graph. 25, 4 (July 1991), 157–164.
Appendix I
Rectangular Prism Submerge Scene: [1]
Trapezoidal Prism Submerge Scene: [2]
Rectangular Approximation of Sine Wave Submerge Scene: [3]
Cube-pixel Submerge Scene: [4]
Trapezoidal-pixel Submerge Scene: [5]
Appendix II
Bridget: Scheduled meetings with Henryk, Communicated with mentor and instructors, worked on MATLAB simulation, researched geometric sine wave representation methods, rendered geometric representation pattern simulations
Caelia: Communicated with mentor and instructors, worked on MATLAB simulation, researched blue noise implementation methods, rendered blue noise pattern simulations
Brian: Communicated with mentor and instructors, worked on MATLAB simulation, researched alternative mesh generation method with ISET3D and PBRT












