A Comparative Study of Compression Algorithms for Multi-Channel Image Data
Introduction
Magnetic resonance imaging (MRI) is a standard medical technique used for imaging parts of the body to visualize detailed internal structures. Providing accurate and good contrast between various soft tissues of the body, this imaging mechanism is applied frequently in several applications concerning cancer detection. However, this system requires a significant amount of storage space in order to save the p-files that the MRI scans are formatted in. In addition, because of the sensitivity of the data, no information can be lost while storing these files.
P-files consist of spiral pulse sequence diagrams of the scan split up in various echoes, slices and receivers. In MRI, the raw data consists of the digitized data measured for a given echo from a given slice of tissue. The echo signal amplitude induced in the receiver coil is digitized as a function of time and represented with complex values. The system used in our research consists of 2 echoes, 41 slices and 32 receivers.
To attack the obstacle of limited memory space, we applied the following compression algorithms in our research: Huffman Coding, Arithmetic Coding, Differential Pulse-Code Modulation (DPCM) and Discrete Cosine Transform (DCT).
Methods
Huffman Coding
Huffman coding is an entropy-encoding algorithm that is optimal for a symbol-by-symbol coding with a known probability distribution. The biggest advantage of this method for our particular application is that it is lossless and assigns a prefix-free code for each unique symbol. For these reasons, we utilized Huffman coding as our default entropy-encoding algorithm throughout our research.
Arithmetic Coding
Arithmetic coding is another lossless encoding algorithm. Similar to Huffman coding, frequently used characters are stored with fewer bits and conversely, more bits are assigned to infrequently used characters. However, this method has better compression capability due to its ability to combine an arbitrary number of symbols for more efficient coding.
The general idea of this coding algorithm is representing the sequence of data values as a rational number between 0 and 1. First, an interval is initialized to [0,1]. The encoder divides this interval into sub-intervals, which represent fractions of the current interval proportional to the probability of the data values. This interval is updated based on the current value, and the process is repeated for the rest of the symbols. The final interval identifies the data symbols. With the same probability model and resulting interval, one may reconstruct the original sequence.
DPCM
Differential Pulse-Code Modulation (DPCM) is an encoding method that provides good compression ratios when used on signals that have correlation between successive samples. The MRI p-files are perfect examples of data that have the mentioned correlation. This compression method can be done in two ways: intra-frame coding and inter-frame coding. For intra-frame coding, spatial redundancy is exploited, whereas for inter-frame coding, temporal redundancy is exploited. The former is executed by taking the difference between the neighboring pixels of the same frame, and the latter is performed by taking the difference between the values of the same pixel in two consecutive frames.
In our implementation, we chose to implement both intra-frame and inter-frame coding. For the inter-frame coding, we first compute the difference of the neighboring pixels in the horizontal (i.e. the temporal) direction, and then perform Huffman or Arithmetic coding on it. For intra-frame coding, we first compute the difference between pixels of two matrices from various slices and echoes and perform entropy coding on the result. In this case, one matrix is directly compressed using entropy encoding and the other matrix is replaced by the difference matrix which is entropy coded.
DCT
The Discrete Cosine Transform (DCT) is widely used in image compression as it is computationally efficient, easily implementable and achieves a compression factor that is comparable to some of the optimum transforms, such as the Karhunen-Loeve Transform (KLT) [2]. Additionally, the DCT decorrelates the input signal in a data-independent manner. For these reasons, we find the DCT being worthy of comparison in our study. However, the major downfall with this compression method for our particular application is that its quantized output is only perceptually lossless.
In our implementation, we first apply the DCT-II with blocksizes of 2, 8 and 32. We then apply a uniform quantizer with a stepsize of 1, since we want to preserve as much information as possible. The probability mass function is constructed for each unique quantized DCT coefficient, and from this, we perform entropy coding to obtain a bitstream representation of the data.
System Overview

For the research, the p-files are obtained from the Center for Neurobiological Imaging at Stanford University [1]. This data is read into Matlab one slice, receiver and echo at a time. Each combination of these three parameters presents a matrix of size 4866 x 80, 4866 representing the image point, 80 representing the time, or frames. This matrix is inputted into our selected encoder and compressed. This compressed format is stored along with the unique values present in the matrix and their corresponding frequencies. In order to read the original information out, each encoded matrix is run through the respective decoder and reconstructed. Once all of the matrices are processed, the reconstructed p-file may be assembled. A detailed diagram of the system is shown in figure 1.
Evaluation Methodology
During our analysis we are mainly interested in two important features of the algorithms: compression ratio and execution time.
Compression Ratio: This is the ratio between the original size of an individual matrix and the compressed size of that matrix. To find the original size of the matrix we find the minimum size needed to store it. First the range of individual terms in the matrix is obtained which is around 1,000. This means that most programs assign each element in the matrix as a 16 bit signed integer. (8 bits can save 256 values, and the next possible assignment in most programs is 16 bits). There are 4866 * 80 complex numbers in a matrix. So, this gives us an original size of roughly 1.5 MB per matrix.
In this report compression ratio is the ratio for each individual matrix. We run the tests for several matrices and average the values.
Execution time: We measure the time required to encode and decode each matrix and evaluate our algorithms based on this execution time. The execution times we present in several of the graphs below have an error of a few seconds; variable CPU usage while running the tests cause this error.
In this report, execution time is the time taken to compress each individual matrix. We run the tests for several matrices and average the values.
Set-up of encoder
Before encoding the matrices, we investigate different set-ups of the matrices to obtain a dataset that results in a good compression ratio in a reasonable amount of execution time. First, we split all matrices into their real and imaginary components and encode them separately.
- Individually: In this setup we encode all matrices individually without making any changes. The compression ratio and execution time from this setup are used as the benchmark to analyze the results obtained from other setups.
- Concatenate two matrices: The values attained from the MRI scans are very similar across multiple matrices. The aim of this setup is to utilize this property to attain a better compression ratio.
- Split individual matrix: Dealing with large matrices increases the time required to encode them. We use this setup to analyze if we can perform the encoding significantly faster while still maintaining the compression ratio.
- DPCM (time difference): While performing the MRI scans the frequency values are attained at different times and saved. One of the axes of an individual matrix is the number of frames or in other words, the values attained at different times. In this setup we take the difference of consecutive samples and encode the difference matrix. We encode the first column separately.
- DPCM (echo/slice difference): In this setup we try to utilize the spatial redundancy between matrices. The difference between the two echoes received with the same slice and receiver are encoded to utilize the spatial redundancies between them. Similarly, signals received from consecutive slices with the same echo and receiver are encoded in a similar way.
- DPCM (time difference + concatenate two matrices): In this setup we try to utilize the benefits of both the time difference DPCM and the concatenation of two matrices to get a better compression ratio.
Huffman Encoder and Decoder
The execution time of the built in compression algorithms in Matlab are not at all practical for compressing the data files from the MRI scans in real time. We have tried to tackle this problem by using some optimization techniques.
A Huffman encoder generates a set of prefix codes for all of the unique elements in a data-set. These codes then replace the values in the original data-set. In our algorithm we parallelize this replacement method by replacing all the unique elements in the matrix by their corresponding code at once.
We also improve the execution time for the Huffman encoder by using a binary tree (in the reverse order) to generate the code table. A binary tree implementation is ideal for generating the code table as the algorithm is done recursively by generating the normalized frequency for every parent node. The tree is then traversed from root to leaf to get the codewords.
Huffman decoding is a highly sequential process and hence the implementation is very time-consuming. To overcome this problem, we use a binary tree structure based on the code table. We start by generating a binary tree with only selected branches, i.e. branches which appear as codes in the code table. We then traverse the tree for each bit in the bit-stream to reach the right leaf node. In this way, we reduce a lot of comparisons and improve the decoding execution time.
Results
Entropy Encoding
In this section, we look at the bit-rates achieved by different entropy encoders and compare them to the entropy of the data-set. It can be seen from table 1 that both Arithmetic coding and Huffman coding obtain bit-rates that are comparable to the entropy with Arithmetic encoding performing slightly better than Huffman encoding.
| Bit Rate | |
|---|---|
| Entropy | 7.4552 |
| Arithmetic | 7.4553 |
| Huffman | 7.4882 |
After attaining the bit-rates, we look at the compression ratios and execution times for both entropy encoding techniques. We use the following built in Matlab functions for the coding techniques: "huffmanenco" and "huffmandeco" for Huffman coding and "arithenco" and "arithdeco" for Arithmetic coding. In addition to these two methods, we also compare the results with the additional Huffman encoder we introduced in the system overview section.
From the plot in figure 2 we see that the built-in Huffman encoder takes around 1400 seconds to encode a single matrix. While significantly better, the Arithmetic encoder requires around 150 seconds for encoding a single matrix. The execution times of both of these methods are not at all practical. This is why we felt the need to use a different encoding technique for the Huffman encoder, which has a lot of potential for parallelization. With this Huffman encoder we reduce the execution time significantly to around 7 seconds per matrix.
Similar to the bit-rates obtained earlier, the compression ratio of the Arithmetic encoder is higher than that of the Huffman encoder. However, while taking the execution time into consideration, the new Huffman encoder is much better and more practical.

DPCM
To understand the benefits of DPCM, we first construct the difference matrix by taking the differences between corresponding samples in the time scale. This utilizes the temporal redundancy in the data. We then compare the entropy of this new difference matrix with the entropy of the original matrix. We repeat this for several matrices, Huffman encode them, and attain the bit-rates achieved. The results are presented in table 2.
| Achieved Bit Rate | Entropy | |
|---|---|---|
| Original | 7.0141 | 6.9760 |
| DPCM | 5.5874 | 5.5499 |
From the table we can see that the entropy of the new matrix after performing DPCM is less than that of the original matrix. The achieved bit-rates closely match the entropy of the data sets. In conclusion, by reducing the entropy of the matrices we can achieve a much better compression.
Progressing from the conclusion made on the DPCM bit rates, we now look at the histograms of the data taken before and after DPCM. The histogram of the difference matrix (after DPCM), as seen in the bottom subplot of figure 3, shows a smaller range of values with higher frequencies as compared to the much wider and flatter histogram of the original matrix. The histogram of the difference matrix also has fewer unique values. These two properties make the DPCM matrix a much better candidate for getting higher compression results.

Set-up Comparison
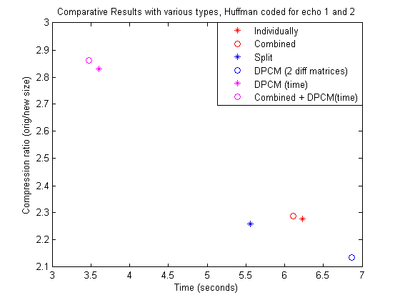
The following four plots (figures 4, 5 6 and 7) present comparative results with various setups that are entropy coded with either Huffman or Arithmetic. While comparing the Arithmetic and Huffman encoders, we can see that Arithmetic encoding gives better compression ratio for all the setups while the Huffman encoder gives a slightly less compression ratio but performs much faster. We will now discuss each of the setups below:
Individual: We use the values for the compression rate and execution time achieved in this setup as the benchmark.
Concatenate 2 matrices: In this setup we see that the compression rate increases slightly. This is because when we combine two matrices, the probability distribution of the data set changes. We get a few values with higher frequencies. However, we also get more unique values. Hence, we do not see a significant increase in the compression ratio. We also don't see a significant change in the execution time. The execution time is generally the same when we concatenate two matrices.
Split individual matrix: In this setup we can see that the execution time does reduce as we had expected, but due to the division of the matrix the probability distribution changes which results in a worse compression ratio.
DPCM (time difference): In all of the figures in this section, we can see that taking the difference between two consecutive samples in the time axis gives us a very good compression ratio. This shows that there is a lot of temporal redundancy in the data.
DPCM (two matrices): In figures 4 and 6, we take the difference between two echoes (from the same receiver and slice). In figures 5 and 7, we take the difference between two consecutive slices (from the same receiver and echo). Encoding the differences for the two echoes does not give us better compression ratios. However, when we encode the difference for two consecutive slices we see that the compression ratio improves slightly in some cases, hinting that there might be some spatial redundancy between consecutive slices.
DPCM (time difference + concatenate two matrices): This incorporates the benefits of the time difference and concatenation of two matrices setups. We can see that the compression ratio increases as compared to the ratio attained by using only DPCM (time difference). Similarly, the execution time stays the same, making this setup the best among all of the different combinations.
 |
 |
 |
 |
From all the different setups we can see that DPCM (time difference) gives the best results. Concatenating two matrices after performing DPCM improves the compression ratio and has a slight improvement in time in most cases. Similarly, consecutive slices show more spatial redundancy than corresponding echoes. So, we now use these properties to see if we can use more than 2 matrices and get the same positive effect. From figure 8 we can see that concatenating matrices from consecutive slices and applying DPCM time difference on the combination before Huffman encoding, gives the best result in terms of both the compression ratio as well as the execution time. Concatenating four matrices results in a slightly higher compression ratio, but the size of the matrix makes it more time-consuming to encode. This is mainly because the larger matrix size results in larger bit-streams as the number of elements in the matrix increases. One of the major bottlenecks in our implementation in terms of execution time is the process of concatenating strings to form a bit-stream. Hence, the execution time increases.

DCT
In terms of the DCT, our goal is to see if the compression ratios outperform all the other algorithms and that the DCT maximum error is still somewhat manageable. In table 3, we see that the maximum errors with respect to the different matrix block sizes we use are very low, since the range of the data values vary from ~-500 to ~500.
| Block Size | 2 | 8 | 32 |
|---|---|---|---|
| Max Error | 1.000 | 1.5250 | 1.7449 |
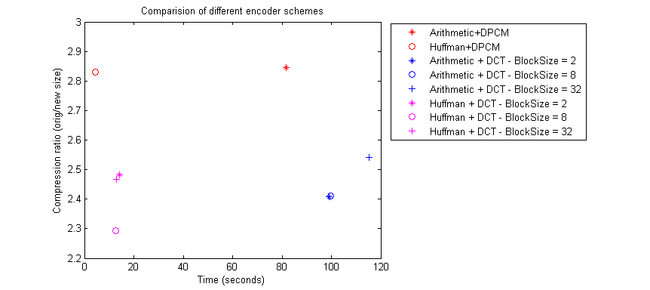
Knowing that the maximum DCT error is somewhat inconsequential, we investigate the compression ratios of the various DCT combinations with some of the entropy coding setups mentioned earlier. From figure 9, we conclude that Huffman + DPCM encoder still outperforms all of the DCT combinations in terms of both execution time and compression ratio.
Figure 9 shows that for DCT with a uniform quantizer step size of 1, the compression ratio is not significantly high despite introducing some errors. Thus, we conclude that the DCT needs a larger quantization step size to have a higher compression ratio. However, based on the expected increase in error, careful consideration has to be made to get the optimum step size while maximizing the compression ratio.
Decoders
We finally look at the execution time required for decoding the compressed matrices. The values for some of the set-ups are presented in tables 4 and 5. From the tables, we can see that DPCM with time difference gives the best execution time among all of the different coding schemes considered.
| Coding Scheme | Execution Time |
|---|---|
| Huffman | 12.21 s |
| Huffman + DPCM | 9.95 s |
| Huffman + DCT (2) | 11.68 s |
| Huffman + DCT (8) | 11.63 s |
| Huffman + DCT (32) | 13.4 s |
| Coding Scheme | Execution Time |
|---|---|
| Arithmetic | 123.4 s |
| Arithmetic + DPCM | 102.2 s |
| Arithmetic + DCT (2) | 114.8 s |
| Arithmetic + DCT (8) | 116.6 s |
| Arithmetic + DCT (32) | 133.5 s |
Conclusions
In this project, we compared different compression algorithms to determine the algorithm that is best for compressing data measured from MRI scans. Based on our results, we found that Arithmetic coding’s compression ratio surpassed that of Huffman. However, because the execution time of Arithmetic is radically longer than Huffman’s and the compression ratios of the two are comparable, we concluded that Huffman coding is better overall.
When incorporating DPCM into our encoding algorithm, we found that the data showed a lot of temporal redundancy, while we couldn't find any convincing result showing significant spatial redundancy. Two consecutive slices had more spatial redundancy than two corresponding echoes, but even this redundancy wasn't very significant. Based on our analysis for the lossless algorithms we can conclude that Huffman + DPCM (in the time frame) gives the best results.
We also found that performing DPCM by utilizing the temporal redundancy in the matrices, concatenating them and performing Huffman coding improves the compression ratio as well as the execution time for the encoding of the matrices. The best result was obtained when we concatenated two matrices. Extending this further and concatenating four matrices results in a better compression ratio but increases the execution time.
Lastly, we integrated DCT into our system using a quantizing step size of 1 and block sizes of 2, 8 and 32. By using a small quantizing step, we saw that the errors due to DCT were very small, but despite the errors DCT did not perform better than the lossless algorithm with DPCM. Different block sizes did not show any significant difference in terms of the compression ratios attained.
So, comparing all of the different setups and algorithms, we conclude that Huffman coding using temporal redundancy of the data is the best encoder in terms of both compression ratio as well as the execution time.
Future Work
From this project we can see that there is a lot of potential of using lossless compression algorithms to compress the data attained from MRI scans. Building on the findings of this project, we would like to additionally look into correlations within echoes, receivers and/or slices by working with more DPCM combinations or possibly looking into other compression algorithms that rid temporal redundancy. In addition we would also like to look at Adapative Huffman Coding techniques to encode data as soon as they are obtained from the MRI scans.
During the project we have mentioned several times that Arithmetic encoder performs better than Huffman encoder when we look at the compression ratios. Thus, clever techniques aimed at shortening the execution time of the Arithmetic code would provide us with an algorithm that has more appealing results, and possibly ones that surpass Huffman coding.
We were able to significantly reduce the execution time for both encoding and decoding the matrices by executing several optimization techniques. However, the execution time taken by our algorithm is still not ideal for practical use. The computation time can be decreased if we implemented our system in C or Python, because there are certain Matlab functions, such as bin2dec and concatenation of strings which slow our algorithm; the corresponding functions in C are much faster.
Acknowledgement
We would like to thank Bob Dougherty from the CNI research laboratory at Stanford, for providing us with the data for our research and guiding us throughout the project, and Atsushi Takahashi for providing us with the initial code to read in the p-files to Matlab.
We would also like to thank Professor Brian Wandell for his valuable guidance during the course of this project and Dr. Joyce Farrell for helping us decide the framework for our project.
References
- Center for Neurobiological Imaging (CNI), Stanford University. https://afs.stanford.edu/?path=/afs/ir/users/b/o/bobd/shared/pfile_project
- N. Ahmed, T. Natarajan, and K. R. Rao, “Discrete cosine transform,” IEEE Trans. Compiti., vol. C-23, pp. 90-93, 1974.
- J. Lee, S. Sagel, R. Stanley, and J. Heiken, Computed Body Tomography with MRI Correlation, vol. 1, 2006.
- Langdon, G. G.; , "An Introduction to Arithmetic Coding," IBM Journal of Research and Development , vol.28, no.2, pp.135-149, March 1984 http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=5390377&isnumber=5390374
- Huffman, D.A.; , "A Method for the Construction of Minimum-Redundancy Codes," Proceedings of the IRE , vol.40, no.9, pp.1098-1101, Sept. 1952 http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=4051119&isnumber=4051100
Appendix
Appendix I
All the Matlab codes and functions used in this project can be found in the following file:
Appendix II
Work Division: The three of us believe that we were all equally involved in the project. All three of us were involved in writing the codes, and preparing the presentation and the wiki page. A very rough work division is presented below:
Nirabh Regmi: DPCM, Arithmetic Coding, Different set-up implementation, Report, Presentation
Tulika Shruti: Huffman Code table generator, Huffman Decoder, Top level code implementation and commenting all the Matlab files, Report
Audrey Wei: Huffman Encoder, DCT, Top level code implementation, Report, Presentation