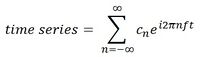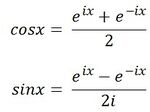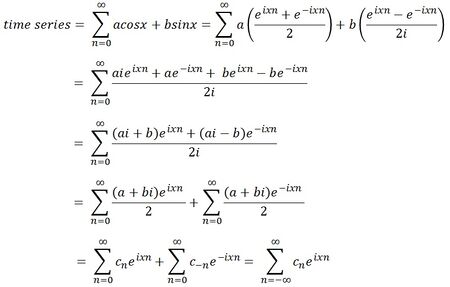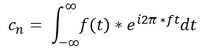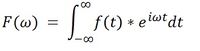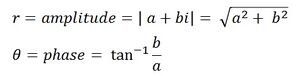Fourier transform math

This page describes some of the math you need for the Fourier transform, as well as deriving some of the formulas you might see thrown around. I'm not a math person, so this is not meant to be as accurate or precise as you will probably see elsewhere. I am including many links to tutorials I found useful in this process.

Fourier Series

Any repeating waveform can be written as an infinite sum of sine and cosine waves at frequencies from 0 to infinity. Each sine and cosine wave at each frequency will have a coefficient, or amplitude, that shows how much that sine and cosine wave contributes to describing the repeating waveform. For example, suppose we have a waveform that has a lot of "sine wave at f = 3" character. The coefficient of the sine wave at f = 3 will thus have a large coefficient.

The whole 0 to infinity number of frequencies looks kind of freaky, but it's basically just saying that the more sine and cosine waves you add to your Fourier series, the better you can describe the repeating waveform. This tutorial has a nifty flash program that lets you make a repeating waveform and then reconstruct it with a bunch of sine and cosine waves. The more waves at different frequencies you add, the more the your Fourier series looks like the repeating waveform. This tutorial is a really good way of "visually" proving the Fourier series to yourself; if I could prove the math to you, I wouldn't be writing this page.

Written as phase shifted cosine

Sometimes the Fourier series is written like this:

This equation is mathematically equivalent to the first one, and can be derived from a trigonometric identity, Rcos(x-ph) = Rcos(ph)cos(x) + Rsin(ph)sin(x). The coefficient c = sqrt(A^2 + B^2) and phi = arctan(b/a). The advantage of this formulation of the Fourier series is that if your waveform is shifted in time (to the left or right), you don't have to re-derive all the coefficients. The only parameters that changes when the wavelength shifts left/right is the phase.

Written using Euler's Formula

A third way of writing the Fourier series is:

This version looks really complicated because of e and the imaginary numbers, but it says the same exact thing as the first two versions above: any repeating waveform can be written as a sum of sine and cosines at different frequencies. In this case, the term "e^iwt" term is just the sine and cosine wave rewritten using Euler's formula, e^ix = cos(x) + isin(x). This might seem like a big jump from the sines and cosines we were using earlier, so below I'm including how we go from one to the other. Feel free to skip this part if you're comfortable with this equation already.

First, using some basic algebra and Euler's formula, e^ix = cos(x) + isin(x), and its conjugate, e^-ix = acosx - isinx, we can rewrite cosine and sine in terms of e's:

Going back to our first formulation of the Fourier series, we can substitute these two equations for sine and cosine and then re-arrange some terms:

Even though this formulation of the Fourier series is the least intuitive looking, it is actually the most frequently used version. The Fourier coefficient is c = a + bi. Just like before, the Fourier coefficient tells us how much a sine/cosine wave characterize the repeating waveform. The larger the Fourier coefficient, the more the sine wave at that frequency characterizes the waveform.

Finding the Fourier coefficient

So now we've got a bunch of sine and cosine waves (written using Euler's formula). How do we find the Fourier coefficient which tells us how much to "weight" each wave? Let f(t) be the repeating waveform, then for any sine/cosine wave e^i2pi*nft:

This equation also looks really intimidating! But remember that the e^whatsit is just a sinusoid at a certain frequency, f(t) is the repeating wave form, and c is just a complex number of the form a + bi. The integral from negative infinity to positive infinity is just a mathematical way of saying, "Let's find the correlation between our repeating waveform and some sinusoid." A large correlation indicates that a sinusoid really characterizes the repeating waveform, which is what I previously said the coefficient says.

How does finding an integral of a product give you a measure of correlation? From high school, you know that you integrate to find the area under a curve. A really simple of way of thinking about this equation then is that if a sinusoid and the waveform are correlated, then the product of the areas under their curves will be positive. If that didn't make sense, watch this guy's video. He explains it much better.

Discrete Fourier Transform

So then what is a Fourier Transform? The Fourier Transform takes a waveform in the time domain and transforms it to the frequency domain. The time domain is typically how we think of our signal (repeating waveform, etc): at different points in time, the signal has a different magnitude. If we plotted the signal in the time domain, the x-axis would be time and the y axis would be some value of the signal.

The frequency domain is a way of representing the original signal in terms of its frequency components. Instead of time on the x-axis, we have frequency. Instead of signal magnitude on the y-axis, we have a measure of the power at the frequency, which is just the amplitude of the sinusoid at that frequency. how do we get these amplitudes? Remember how we found the Fourier coefficients in the previous section? Finding that coefficient at a particular frequency IS taking the Fourier transform at that frequency. Taking the Fourier transform of a signal is just finding the Fourier coefficient for all the sine waves at all the possible frequencies:

F(w) is just the set of all the Fourier coefficients for all the sinusoids at different frequencies. How many different frequencies? The Fourier series says that any repeating signal can be written as an infinite number of sinusoids. However, in fMRI, we are discretely sampling our data (every TR, typically ~2 sec), so there is an upper limit to the number of frequencies we can use: #times sampled/2. This is the Nyquist frequency, which sets the maximum resolution for a discretely sampled signal. So we don't have an infinite number of Fourier coefficients. We have #times/smpled + 1 coefficients.

Phase and amplitude

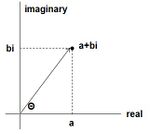
The Fourier coefficient is kind of a mysterious number. It contains both phase and amplitude information, but how do we get it? First, we know the Fourier coefficient is a complex number a + bi. Imaginary numbers are kind of confusing, but they're really just another "axis," like the x-axis or y-axis. So a complex number just represents a point in the complex plane, where one axis is the real component while the other is the imaginary component.

If a complex number is just a point in space, we can also write it in polar coordinates: a radius r, extending from the origin to a+bi, and an angle theta, the angle between the real axis and the radius r. The radius r is the amplitude of the sine wave and the angle theta is its phase.