Back to Psych 204 Projects 2009

Correction of magnetic field distortion in EPI images

Magnetic field inhomogeneities are the most common cause of distortions in fMRI images, which make matching of data to the high-resolution structural images difficult. Various methods have been proposed to correct for this distortion. For this project, some of these methods were examined and tested on EPI data. In particular, a toolbox based on magnetic field mapping methods and developed for the SPM software environment, was tested on EPI data provided by the VISTA lab. Furthermore, the toolbox was integrated better into the mrVista software environment to make it work without installing SPM. Also, attempts were made to quantify how well these methods worked. Finally, a small collection of relevant literature on the topic was collected.

Background

Those familiar with the theoretical background of magnetic field distortions may skip this section. The material was mostly gathered from Functional Magnetic Resonance Imaging by S.A. Huettel, A.W. Song and G. McCarthy and from the manuals included with the SPM FieldMap toolbox.

Causes of field disturbances

The main reason for magnetic field disturbances in MRI imaging is the different magnetic susceptibility of the different materials in the brain. A material's magnetic susceptibility is the degree of magnetization of the material when an outside magnetic field is applied. In areas of the head where two materials with different susceptibilities meet, especially near cavities such as the sinuses in the frontal lobe or the ear canals in the temporal lobes where you have a junction of water and air, the magnetic field will behave in a way that looks quite erratic. The exact disturbance of the field will behave on the size and shape of the cavity and its orientation relative to the magnetic flux, and will thus change should the subject move in the scanner. Disturbances can also arise when you have blood flow in nearby large vessels, such as around the sagittal sinus, although this effect is less of a problem.

The effect of field disturbances on EPI images

During EPI imaging, each voxel in the object being imaged emits a series of echoes that identify its position - the frequency within the echoes gives its position in the frequency encode direction, and the phase difference between consecutive echoes gives its position in the phase-encode direction.

Field disturbances at a particular point in space cause the field to be slightly different than what would be expected under normal conditions at that point. Then, during read-out, its signal will have a slightly different frequency than normal (we recall that the Larmor frequency varies linearly with field strength) so when the image is constructed the corresponding voxel will be displaced in the frequency encode direction. The magnitude of this displacement depends on the magnitude of the field disturbance. Since the disturbance magnitude is usually very small compared to the gradient field, this effect in the frequency encode direction is usually negligible. However, this change in frequency also leads to a change in phase difference between consecutive echoes. This causes a displacement in the phase encoded direction as well, and since this disturbance affects the measurement through the whole read-out but the gradient is only applied for a short time, this displacement can be considerable and can not be neglected.

The effects from this can be minimized by making the read-out time shorter or applying the gradient for a longer time period, but this generally results in lower image resolution unless more advanced techniques of spatial encoding are used. That leads us to correcting for these errors using magnetic field map techniques. Other methods, such as the use of shimming coils, exist for correcting these errors as well but those methods are beyond the scope of this project.

Magnetic field mapping

A field map of the main magnetic field is created by acquiring two images of the signal phase with slightly different echo times. The difference between the phase images at each voxel is proportional to the strength of the field. If the field is completely uniform, the phase difference induced by the different echo times will be the same in all voxels and the resulting image will have a uniform magnitude. If the field is not uniform, the two images should show a difference in phase, which can be attributed to a longer time for disturbance induced phase to evolve when the echo-time is longer. So the difference between the two images will tell us how fast the signal phase changes, which gives us a frequency map through the equation

$\Delta f={\frac {\Delta \phi }{2\pi \Delta t}}$

The frequency map can then be used to generate a field map through the Larmor equation:

$\omega =-\gamma B$

The field map can then, in theory, be used to resample the distorted image so that all field distortions are corrected for.

Practical problems with magnetic field mapping

Phase wrapping

One problem with the approach described above to produce the frequency map, and subsequently the field map, is that $\Delta \phi$ is periodic (with period $2\pi$ ) in its effect on the image, i.e. there is no way to tell whether a perceived phase difference between the two images is truly $\Delta \phi$ or $\Delta \phi +2\pi$ . This can lead to wrong estimations of frequency shift, for example if the true phase difference is $13\pi /6$ and the echo time difference is 20 ms, then the correct frequency shift would be about 58 Hz, but there would be a danger of determining the frequency shift to be $\pi /6$ and thus get a frequency estimate of 34 Hz.

This can be dealt with using a short enough echo-time difference for it to be highly unlikely that a phase difference larger than $\pi$ would ever be obtained. However, this leads to most values of phase shift being very low and hardly distinguishable from noise.

Another approach is to use phase unwrapping - add/subtract a value of $2\pi$ whenever we see a jump in phase of more than $\pi$ .

However, using this method, whenever an error is made (which most often happens in regions of low signal-to-noise ratio, such as in air or bone), then the error will propagate through all subsequent voxels. Therefore, it is quite important to make every effort to prevent such errors. This is usually done either by starting the unwrapping in an area with high SNR, so any errors will likely occur late in the process and affect fewer voxels, or by dividing the brain into regions, where each region should have a small face shift, and the use the unwrapping procedure on the region boundaries. The latter method is used exclusively in this project.

Choice of phase-mapping sequence

In theory, it should not matter whether the method of phase mapping described above uses an EPI sequence or a non-EPI sequence. Using EPI measurements for the fieldmap gives us a fieldmap in distorted space, which then has to be inverted and should then theoretically be the same as a fieldmap based on non-EPI data. However, this is most often not the case, and the reasons are not well known. However, empirical evidence suggests that EPI-based fieldmaps give better results than the alternative. This project solely uses EPI based fieldmaps since other data was not available.

Methods

The FieldMap toolbox for SPM utilizes the methods described above. In this project, a program was made to make use of this toolbox easier for users of mrVista who might be unfamiliar with SPM. The program was called mrFieldMap.

How to use the software

Once mrFieldMap has been installed, either by extracting the zip file provided at the bottom of this page on the hard drive and adding its path in Matlab or by checking out a version of the VistaSoft repository which includes mrFieldMap, the software can then be started by typing mrFieldMap at the Matlab command prompt. The following image will appear:

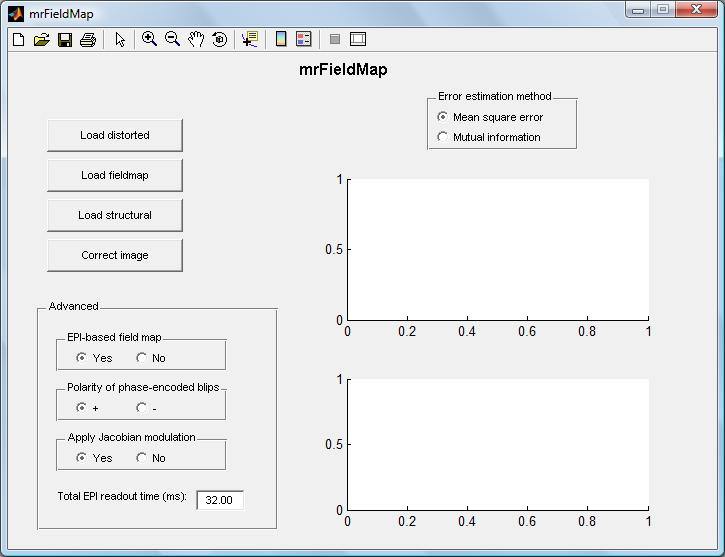
Normally, one would begin by clicking the "load distorted" button, which allows the user to load the distorted EPI image which needs to be corrected. By clicking the "load field map" button, the user can load the field map which is used to correct the image. The button "load structural" allows the user to load a structural image which should be undistorted. This is not a necessity, but is useful to estimate how well the unwarping algorithm is working. The fourth button, "correct image", uses the field map to unwarp the distorted image and produce a new image more similar to the field map.
The user can also specify whether the field map is EPI based, in which case the unwarping must take into account that the field map itself is distorted. Theoretically this should not be a problem but in practice, however, unwarping an image using a warped EPI based field map (by unwarping the field map first) does produce a slightly different image than unwarping it using a non-EPI based field map. The theoretical reasons for this are unclear but imperical results suggest it is generally better to use an EPI based field map.
Also, one can specify whether the data acquisition was done with positive or negative phase encoding blips - basically whether the phase increments in the phase-encoded direction are positive or negative. If the wrong value is chosen, the unwarping will be in the wrong direction and the resulting image will actually be more distorted than the original.
The user can choose to apply Jacobian modulation in the unwarping. This increases the intensity in the unwarped image of voxels which are stretched and decreases the intensity of compressed voxels.
Finally, one can enter the readout time of the EPI measurement. This is used to convert the field map, which is in units of Hz (i.e. it is in the frequency domain) into a voxel displacement map (i.e. to the spatial domain) by simple multiplication. This is defaulted to 32 ms.

As soon as an image has been loaded using one of the three loading buttons, a second GUI pops up, displaying the loaded images:

This GUI is an altered version of the mrViewer GUI and allows the user to choose any slice along any of the three main axis. The user can also switch between any of the loaded images and the unwarped image, as well as an image showing the difference between the unwarped image and the structural image, to make the estimation of the performance of the unwarping algorithms easier.

Once the correction button in the main GUI is clicked, the unwarped image is automatically saved into the same directory as the distorted image, and two graphs appear, showing the difference between the distorted image and the structural image on the one hand, and between the unwarped image and the structural image on the other hand (the voxel displacement map described above is also saved into the same directory). The user can choose between simple mean square error or the mutual information between the images as the error metric.

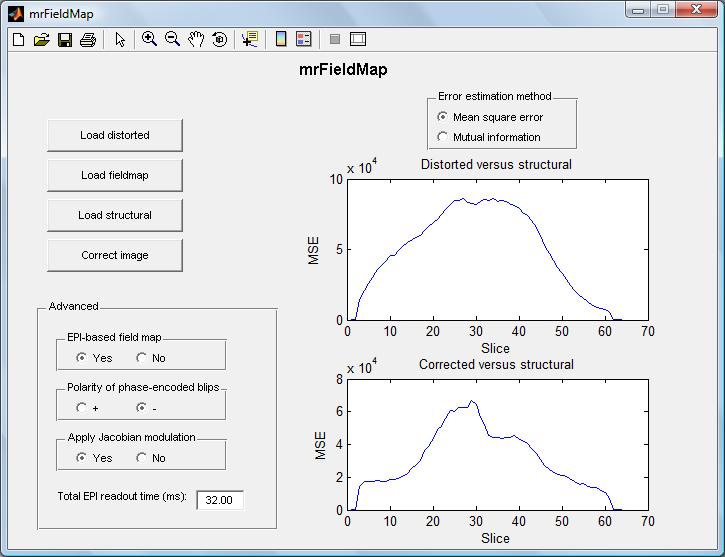
These error plots should not be regarded as exact science - the exact numerical values on the plots don't have a clear meaning since the slices are scaled to have the same mean vale - but if the unwarped image clearly has a lower mean square difference from (or higher mutual information with) the structural image than the distorted image does, it seems reasonable to assume that the unwarping is serving its purpose to some degree.

Results

The program was tested on a squashed phantom image and a stretched phantom image, both provided with the SPM FieldMap toolbox, as well as on an EPI image of an actual brain provided by the VISTA lab.

Squashed phantom image

Unwarping of squashed phantom image

Included in the SPM FieldMap toolbox is an EPI image of a ball which has been distorted in the image acquisition to become more oval-shaped. Also included are the corresponding fieldmap and structural image. When unwarping this image, all parameters can be kept at their default values, except the phase blip value must be set to negative. The results are shown below:

As can be seen from the images, the unwarped image looks more spherical shaped like the structural image. As can be seen from the differential image, the difference between the two shapes is highest at the edges but overall the difference seems to be relatively uniform, indicating a successful unwarping.

Estimates of unwarping quality for squashed phantom ball

Using the main mrFieldMap GUI, the mean square error between the slices of the distorted image and the structural image as well as between the unwarped image and the structural image can be examined. The same can be done for the mutual information between the images. The results are shown below:

As can be seen from the images, the mean square error for the unwarped image is considerably lower than for the distorted image, indicating successful unwarping. The mutual information, however, seems to be roughly the same for the two images. This seems to indicate that the mutual information method is not sensitive enough for small distortions as we see here and is therefore unsuitable for measuring degree of success in unwarping.

Stretched phantom ball

Unwarping of stretched phantom image

The SPM Toolbox also includes a spherical phantom image that is stretched and not squashed. By following the same procedure as for the squashed phantom, the results shown below were obtained:

As can be seen from the images, we obtain much the same results as for the squashed phantom ball. The unwrapped image is more spherical than the original and the difference between the unwrapped image and the structural image seems to be concentrated at the edges of the ball, indicating less than perfect unwrapping. Overall, the unwrapped image clearly is an improvement from the distorted one.

Estimates of unwarping quality for stretched phantom ball

The mean square error and the mutual information were also examined in this case as for the squashed ball. The results are shown below:

Again, we get similar results as for the squashed ball. The mean square error seems to indicate that the unwarping was successful to some degree, but the mutual information with the structural image seems very similar for the distorted and unwarped images, giving little information about the quality of the unwarping procedure.

Brain image

An EPI from a real brain scan was provided by the VISTA lab along with a corresponding field map and structural image. The mrFieldMap software was tested to see if the image could be successfully be unwarped.

Unwarping of brain image

Various combinations of parametric settings were tested for this data set. The most appropriate setting seemed to be EPI based field map with positive polarity of phase blips without Jacobian modulation. The results are shown below:

This time, the result are quite different from the ones in the phantom experiments. The unwarped image becomes quite blurry at the edges and the image seems noisy in general. There seems to be little actual change in shape of the image, although by careful comparison of the distorted image, the structural image and the unwarped image, the shape of the unwarped brain seems to be a little bit closer to the structural than the distorted brain does, although this effect is barely noticeable.
The reasons for this behavior are unclear. Possibly something is wrong with the field map used or the unwarping algorithm doesn't handle very well images with as high a resolution as this one (the phantom images seemed to be of lower resolution).

Estimates of unwarping quality for brain image

The mean square error and the mutual information were estimated for the brain image unwarping as before. The results were as follows:

Clearly, the error estimation graphs are not as helpful as before. We get a huge error (and very low mutual information) for the first two or three slices. The reason for this seems to be that the first few slices of the distorted image and the structural image don't correspond very well to each other. The first slice of the distorted image seems to be completely blank while the first slice of the structural image is not. The second slice for both images also don't seem to make a good match:

So in this case, it is hard to make any sort of estimate based on the error graphs, but at least the MSE graphs and the mutual information graphs seems to correspond well to each other - when we have very high mean square error we have low mutual information.

Effects of wrong choice of parameters

Choosing the wrong values for the warping parameters can have dramatic results on the resulting image. The pictures below shows the effect of choosing the wrong polarity of phase encoding blips for the squashed phantom ball:

The pictures clearly show that the image becomes even more squashed, and the resulting mean square error is worse than before. No noticable difference was observed in the mutual information, however. Furthermore, changing the parameters to non-EPI based field map and/or no Jacobian modulation or tweaking the EPI readout time did not seem to have much effect in this example. Thus, we can conclude that this image is sensitive to the polarity of the phase encoding blips but not as sensitive to the other parameters.

Unwarping of simple images

To examine the effect of unwarping on a simple structure, such as a straight line, a "dummy" image file was created that only consisted of a single frame, i.e. four lines forming a square, at slice no. 32 out of 64. The other slices (and the rest of slice 32) were given small random values at each voxel to represent noise. This image was then unwarped using the field map for the squashed phantom ball. The results were as follows:

The effects of the unwarping are quite interesting in this case. The differences between the distorted image and the unwarped image are quite subtle (and can only be seen by expanding the thumbnails). In the unwarped image, the vertical lines have partially moved a little bit to the outside of the fram, though a faint shadow of the old lines remain. The horizontal lines seem to be unaffected. This seems intuitively correct, since the fieldmap should correct for distortion in the horizontal (i.e. the anterior-posterior) direction.
The error graphs show that the difference between the images spikes at slice 32 which is also what one would expect, since at that slice the frame appears and its lines mostly don't overlap with the structural image.

Some technical comments about the code

The whole set of functions required to run the mrFieldMap software is about 5.7 MB in size (in unzipped format), of which about 3 MB are SPM functions that were too difficult to untangle from the FieldMap code. The software is provided at the bottom of this page. The test images for trying out the code are about 15 MB and are provided in a separate file.
The code can be quite slow to run but that is mostly due to the error estimates that I added. The unwarping algorithms are quite fast. The brain image described above took a much longer time to compute than the phantom images - about 9 minutes compared to about 30 seconds for the phantoms.
The original FieldMap toolbox for SPM had some additional functions that were not included in my application, most importantly the option to create the field map out of the two images. This was omitted mostly because I didn't have data from VISTA lab to test this on, but also for time constraint reasons. Also, in the original toolbox you could choose your method of phase unwrapping as described in the theoretical section of this site. In this project I only used the method of dividing the brain into distinct regions as described in the same section.
Every effort was made to make sure that the software would work on any computer, however I have only tested it on my own computer.

Conclusions

In this project, a program was written to make it easier for users of the mrVista software to unwarp distorted EPI images. This was done by combining elements of a preexisting unwarping toolbox for SPM called FieldMap with a few programs developed in the VISTA lab. Good results were obtained from unwarping images included with the FieldMap toolbox, however, the results for a brain image provided by the VISTA lab were much poorer. The reasons for this are unclear, but reasonable guesses are a faulty field map or limitations in the unwarping algorithms for high resolution images.
The program includes methods to estimate the degree of success in the unwarping, based on either mean square error or mutual information. In general, the mean square error provided a much better estimate of the unwarping quality. However, neither estimate proved very accurate and visual inspection of the unwarped image is probably a better way of estimating how well the unwarping worked.

The effects of choosing the wrong unwrapping parameters were examined and also the results from unwrapping a very simple structure. In both cases, the results were as expected (wrong polarity of phase encoding blips makes distortion worse, unwarping of a simple frame changed its geometry in the same manner as the distorted image when unwrapped).

Finally, a small number of articles on the subject was collected and is listed in the references section of this site.

References - Resources and related work

It is important to note that the bulk of the code used in this project was not programmed by me. I simply took the FieldMap toolbox for SPM, a few pieces of the main SPM code, some functions from the VISTA lab and mutual information algorithms and put these pieces together.

Most of the credit belongs to Chloe Hutton and Jesper Andersson who developed the FieldMap toolbox for SPM. Not only did I use their code extensively, but I also used their excellent manuals to gain a better theoretical understanding of magnetic field map technology.
The VISTA code I made use of was mostly programmed by Rory Sayres.
The Matlab algorithms for determining mutual information were programmed by Hanchuan Peng.
Bob Dougherty and Jon Winawer at the VISTA lab were very helpful in providing data and answering questions.
Most of my theoretical knowledge of EPI, magnetic field maps and MRI in general comes from
- Functional Magnetic Resonance Imaging by S.A. Huettel, A.W. Song, and G. McCarthy.
- The manuals included with SPM and the FieldMap toolbox
- The VISTA lab wiki site
- Lecture notes in the course PSYCH 204A by Brian Wandell and Bob Dougherty at the VISTA lab

The following papers were also helpful and might be of use to anyone interested in learning more about magnetic field maps or EPI imaging technology. The first five papers were instrumental in the development of the FieldMap toolbox for SPM.

Appendix I - Code, Data and Presentation

Code

The mrFieldMap code (without images for testing)

Data

Images for testing the code

Presentation

Slightly revised version of presentation given on Dec. 1st, 2009

2009 Bragi Sveinsson

Contents

Correction of magnetic field distortion in EPI images

Background

Causes of field disturbances

The effect of field disturbances on EPI images

Magnetic field mapping