Bragi Sveinsson

Back to Psych 204 Projects 2009

Correction of magnetic field distortion in EPI images

Magnetic field inhomogeneities are the most common cause of distortions in fMRI images, which make matching of data to the high-resolution structural images difficult. Various methods have been proposed to correct for this distortion. For this project, some of these methods were examined and tested on EPI data. In particular, a toolbox based on magnetic field mapping methods and developed for the SPM software environment, was tested on EPI data provided by the VISTA lab. Furthermore, the toolbox was integrated better into the mrVista software environment to make it work without installing SPM.

Background

Causes of field disturbances

The main reason for magnetic field disturbances in MRI imaging is the different magnetic susceptibility of the different materials in the brain. A material's magnetic susceptibility is the degree of magnetization of the material when an outside magnetic field is applied. In areas of the head where two materials with different susceptibilities meet, especially near cavities such as the sinuses in the frontal lobe or the ear canals in the temporal lobes where you have a junction of water and air, the magnetic field will behave in a way that looks quite erratic. The exact disturbance of the field will behave on the size and shape of the cavity and its orientation relative to the magnetic flux, and will thus change should the subject move in the scanner. Disturbances can also arise when you have blood flow in nearby large vessels, such as around the sagittal sinus, although this effect is less of a problem.

The effect of field disturbances on EPI images

During EPI imaging, each voxel in the object being imaged emits a series of echoes that identify its position - the frequency within the echoes gives its position in the frequency encode direction, and the phase difference between consecutive echoes gives its position in the phase-encode direction.

Field disturbances at a particular point in space cause the field to be slightly different than what would be expected under normal condition at that point. Then, during read-out, its signal will have a slightly different frequency than normal (we recall that the Larmor frequency varies linearly with field strength) so when the image is constructed the corresponding voxel will be displaced in the frequency encode direction. The magnitude of this displacement depends on the magnitude of the field disturbance. Since the disturbance magnitude is usually very small compared to the gradient field, this effect in the frequency encode direction is usually negligible. However, this change in frequency also leads to a change in phase difference between consecutive echoes. This causes a displacement in the phase encoded direction as well, and since this disturbance affects the measurement through the whole read-out but the gradient is only applied for a short time, this displacement can be considerable and can not be neglected.

The effects from this can be minimized by making the read-out time shorter or applying the gradient for a longer time period, but this generally results in lower image resolution unless more advanced techniques of spatial encoding are used. That leads us to correcting for these errors using magnetic field map techniques. Other methods, such as the use of shimming coils, exist for correcting these errors as well but those methods are beyond the scope of this project.

Magnetic field mapping

A field map of the main magnetic field is created by acquiring two images of the signal phase with slightly different echo times. The difference between the phase images at each voxel is proportional to the strength of the field. If the field is completely uniform, the phase difference induced by the different echo times will be the same in all voxels and the resulting image will have a uniform magnitude. If the field is not uniform, the two images should show a difference in phase, which can be attributed to a longer time for disturbance induced phase to evolve when the echo-time is longer. So the difference between the two images will tell us how fast the signal phase changes, which gives us a frequency map through the equation
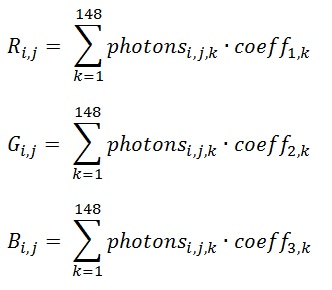[1]
\delta f = \frac{\delta \phi}{2 \pi \delta t}
The frequency map can then be used to generate a field map through the Larmor equation:
\omega = - \gamma B
The field map can then, in theory, be used to resample the distorted image so that all field distortions are corrected for.

Practical problems with magnetic field mapping

Phase wrapping

One problem with the approach described above to produce the frequency map, and subsequently the field map, is that \delta \phi is periodic (with period 2 \pi) in its effect on the image, i.e. there is no way to tell whether a perceived phase difference between the two images is truly \delta \phi or \delta \phi + 2\pi. This can lead to wrong estimations of frequency shift, for example if the true phase difference is 13\pi/6 and the echo time difference is 20 ms, then the correct frequency shift would be about 58 Hz, but there would be a danger of determining the frequency shift to be \pi/6 and thus get a frequency estimate of 34 Hz.

This can be dealt with using a short enough echo-time difference for it to be highly unlikely that a phase difference larger than \pi would ever be obtained. However, this leads to most values of phase shift being very low and hardly distinguishable from noise.

Another approach is to use phase unwrapping - add/subtract a value of 2\pi whenever we see a jump in phase of more than \pi, as shown in the figure below.
\figure

However, using this method, whenever an error is made (which most often happens in regions of low signal-to-noise ratio, such as in air or bone), then the error will propagate through all subsequent voxels. Therefore, it is quite important to make every effort to prevent such errors. This is usually done either by starting the unwrapping in an area with high SNR, so any errors will likely occur late in the process and affect fewer voxels, or by dividing the brain into regions, where each region should have a small face shift, and the use the unwrapping procedure on the region boundaries. Both approaches are tested in this project.

Choice of phase-mapping sequence

In theory, it should not matter whether the method of phase mapping described above uses an EPI sequence or a non-EPI sequence. Using EPI measurements for the fieldmap gives us a fieldmap in distorted space, which then has to be inverted and should then theoretically be the same as a fieldmap based on non-EPI data. However, this is most often not the case, and the reasons are not well known. However, empirical evidence suggests that EPI-based fieldmaps give better results than the alternative. This project solely uses EPI based fieldmaps since other data was not available.

Below is an example of a retinotopic map. Or, to be precise, below will be an example of a retinotopic map once the image is uploaded. To add an image, simply put text like this inside double brackets 'MyFile.jpg | My figure caption'. When you save this text and click on the link, the wiki will ask you for the figure.

Below is another example of a reinotopic map in a different subject.
Figure 2

Once you upload the images, they look like this. Note that you can control many features of the images, like whether to show a thumbnail, and the display resolution.

Figure 3

MNI space

MNI is an abbreviation for Montreal Neurological Institute.

Methods

Measuring retinotopic maps

Retinotopic maps were obtained in 5 subjects using Population Receptive Field mapping methods Dumoulin and Wandell (2008). These data were collected for another research project in the Wandell lab. We re-analyzed the data for this project, as described below.

Subjects

Subjects were 5 healthy volunteers.

MR acquisition

Data were obtained on a GE scanner. Et cetera.

MR Analysis

The MR data was analyzed using mrVista software tools.

Pre-processing

All data were slice-time corrected, motion corrected, and repeated scans were averaged together to create a single average scan for each subject. Et cetera.

PRF model fits

PRF models were fit with a 2-gaussian model.

MNI space

After a pRF model was solved for each subject, the model was trasnformed into MNI template space. This was done by first aligning the high resolution t1-weighted anatomical scan from each subject to an MNI template. Since the pRF model was coregistered to the t1-anatomical scan, the same alignment matrix could then be applied to the pRF model.
Once each pRF model was aligned to MNI space, 4 model parameters - x, y, sigma, and r^2 - were averaged across each of the 6 subjects in each voxel.

Et cetera.

Results - What you found

Retinotopic models in native space

Some text. Some analysis. Some figures.

Retinotopic models in individual subjects transformed into MNI space

Some text. Some analysis. Some figures.

Retinotopic models in group-averaged data on the MNI template brain

Some text. Some analysis. Some figures.

Retinotopic models in group-averaged data projected back into native space

Some text. Some analysis. Some figures.

Conclusions

Here is where you say what your results mean.

References - Resources and related work

Jezzard P and Balaban RS (1995) Correction for geometric distortions in echoplanar images from B0 field variations. Magn Reson Med 34:65-73
Andersson JLR, Hutton C, Ashburner J, Turner R, Friston K (2001) Modelling geometric deformations in EPI time series. NeuroImage 13:903-919
Hutton C, Bork A, Josephs O, Deichmann R, Ashburner J, Turner R. (2002). Image distortion correction in fMRI: A quantitative evaluation. NeuroImage 16:217-240
Jenkinson M. 2003. Fast, automated, N-dimensional phase-unwrapping algorithm. MRM 49:193-197
S. Balac and G. Caloz , Mathematical modeling and numerical simulation of magnetic susceptibility artifacts in magnetic resonance imaging. Comput. Methods Biomech. Biomed. Eng. 3 (2000), pp. 335–349.

Software

Appendix I - Code and Data

Code

zip file with code

Data

zip file with my data

Appendix II - Work partition (if a group project)

Brian and Bob gave the lectures. Jon mucked around on the wiki.